Introduction

Entangled multi-partite states have a pivotal role in quantum technologies based on multiple platforms, ranging from trapped-ions1 to superconducting qubits2. In photonics, over the past two decades, major advances in the generation of multi-photon entanglement have been achieved by exploiting spontaneous parametric down-conversion (SPDC) and free-space apparatuses3,4,5,6,7,8. Very recently, one dimensional linear cluster states were generated on demand through atom-photon entanglement9 or spin-photon entanglement10,11 at high rate9,11 and high indistinguishability10,11. While the complexity of the generated states in some of these works7,8,9 is still unmatched, the long-term viability and scalability lie in harnessing also miniaturization and integration capabilities that chip-based platforms offer.

Consequently, in the last few years, there has been a significant focus on the generation of multi-photon states in integrated circuits, with noteworthy results in the demonstration of reconfigurable graph states in silicon-based devices via on-chip spontaneous four-wave mixing (SFWM)12,13,14,15,16. In these works, the generation of the input state is probabilistic, and thus it can only be heralded but not produced on-demand. An intrinsic issue of this approach is the emission of unwanted photon pairs, whose generation probability is proportional to the average number of generated photons. One has thus to reach a trade-off between large rate and coincidence-to-accidental ratio17.

An alternative approach to the generation of multi-photon states harnesses optically engineered quantum-dot (QD) emitters that operate as on-demand bright sources of indistinguishable single-photons in wavelength ranges well suited for high-efficiency single-photon detectors18,19,20,21. Recently, the potential of such high-performance single-photon sources (SPS) for the generation of multi-photon states has been highlighted with bulk optics22,23 and micro-optics assemblies24. QDs are also compatible with integrated photonic chips25,26,27,28 and, in particular, with glass optical circuits fabricated by femtosecond laser micromachining (FLM)29,30. These devices offer an efficient interfacing with optical fibers, low losses at the QD emission frequencies, and the possibility of integrating thermal phase shifters to achieve full circuit programmability. Thanks to these characteristics, the combined use of QD-based SPS and laser-written photonic processors have demonstrated to be an effective platform for quantum information processing31,32.

In this work, we demonstrate the on-chip generation and characterization of an entangled state using an off-chip on-demand single-photon source. In particular, a 4-photon Greenberger-Horne-Zeilinger (GHZ) state33 has been demonstrated by interfacing a bright SPS, fit for scaling up and for real-world applications, with a programmable laser-written photonic chip.

We achieve a complete characterization of the generated state through the reconstruction of its density matrix via quantum state tomography. By using a semi device-independent approach, we further test non-classical correlations, certify entanglement, non-biseparability, and study the robustness of the generated states to noise. Finally, as a proof-of-principle that our platform is application ready, we show that it can be used to implement a 4-partite quantum secret sharing protocol34. Our approach combines the practical assets of bright QD-based SPS, efficient single-photon detectors, and low-loss, scalable, integrated optical circuits fabricated using FLM.

Results

Path-encoded 4-GHZ generator

Among graph states, GHZ states are striking examples of maximally entangled states that are considered a pivotal resource for photonic quantum computing, since they can be used as building blocks for the construction of high-dimension cluster states35. They are also of interest for quantum communication and cryptography protocols34,36.

In this work, we target 4-partite GHZ states of the form:

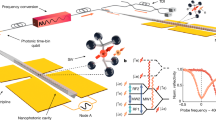
$$\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle =\frac{\left\vert 0101\right\rangle +\left\vert 1010\right\rangle }{\sqrt{2}}$$
(1)

encoded in the path degree of freedom (dual-rail). In Fig. 1 the conceptual scheme of our path-encoded 4-partite GHZ generator chip is depicted. It is composed by a first layer of balanced beam splitters (50/50 directional couplers) followed by waveguide permutations (3D waveguide crossings). The 4-photon input states are created using a high-performance QD based single-photon source at 928 nm (Quandela e-Delight-LA)18 and a time-to-spatial demultiplexer (Quandela DMX6) (see Methods), which initialize the input states to \(\left\vert 0000\right\rangle\). With this scheme, the generation of the GHZ states relies on post-selection, i.e., it is conditioned to the presence of one and only one photon per qubit, which sets the success probability to 1/8. Finally, the chip allows for the characterization of the generated states by means of four reconfigurable Mach-Zehnder interferometers (MZI), each one implementing single-qubit Pauli projective measurements (σx, σy, σz) in the path degree of freedom. The overall system efficiency enables us to detect useful 4-fold coincidence events at the rate of 0.5 Hz with a pump rate of 79 MHz. This is on par with the recent record for generating entangled states in integrated photonics15. Because of the short lifetime of our photons (145 ps), a pump rate of 500 MHz is achievable, which would yield a generation rate >3 times higher than15. Further details about the chip functioning, its manufacturing and the experimental setup are provided in the Supplementary Notes 1 and 2.

Fig. 1: Integrated path-encoded 4-GHZ generator.
figure 1

Conceptual layout. For each qubit i, the upper and lower waveguides encode the computational basis {\({\left\vert 0\right\rangle }_{i}\), \({\left\vert 1\right\rangle }_{i}\)}. The preparation of the state in Eq. (1) along the black dashed line (dots and crosses encoding the \(\left\vert 0101\right\rangle\) and \(\left\vert 1010\right\rangle\) states respectively) is conditioned ("& ” and red arrow) to the detection of one and only one photon (red dot) per qubit. The projective measurements of the tomography stage are performed by four thermally reconfigurable MZIs. One of the phase shifters before MZI1 is also used for controlling the phase θ (Supplementary Note 1).

Full size image

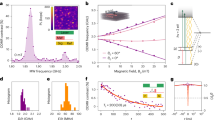
Our photonic chip is reconfigurable, thus it can generate a whole class of GHZ states of the form \({\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle }^{(\theta )}=\left(\left\vert 0101\right\rangle +{e}^{i\theta }\left\vert 1010\right\rangle \right)/\sqrt{2}\), parametrized by an internal phase θ corresponding to the algebraic sum of the optical phases acquired by each photon in the different paths of the preparation stage after the beam splitters (Supplementary Note 1). The phase θ can be controlled with a single phase-shifter localized on one of these paths, as depicted in Fig. 1. To prepare the targeted GHZ states, we use a 2-qubit Pauli projector \({M}_{0}^{(i)}\) for each qubit i ∈ {1,.. , 4} (See Methods for each \({M}_{0}^{(i)}\) definition), and compute the expectation value \(\langle \hat{\Theta }\rangle =\langle {M}_{0}^{(1)}{M}_{0}^{(2)}{M}_{0}^{(3)}{M}_{0}^{(4)}\rangle\). For our class of GHZ states, \(\langle \hat{\Theta }\rangle\) can be used as an internal phase witness as \(\langle \hat{\Theta }\rangle =(\sqrt{2}/2)\cos \theta\), and it reaches its maximum value for the target state \(\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle\) at θ = 0[2π]. Figure 2a shows the measured \(\langle {\hat{\Theta }}_{exp}\rangle\) as a function of the driving power of one of the outer thermal phase shifters of MZI1, and it demonstrates that we have full control over the value of θ in the state preparation. The recorded 4-photon coincidence probability distribution corresponding to our target state is reported in Fig. 2b. We measure the maximal value of \(\langle {\hat{\Theta }}_{exp}\rangle =0.56\pm 0.01\), which is limited by some experimental imperfections discussed in “On-chip quantum-state tomography”.

Fig. 2: Preparation of 4-GHZ states in the path-encoded basis and reconstruction of its density matrix.
figure 2

a A single phase-shifter (see Fig. 1a) is scanned over a ~50 mW range of electrical driving power P. For each value of θ and each 4-qubit state we acquire the 4-photon coincidence rates for 900 s and compute the phase witness \(\langle {\hat{\Theta }}_{exp}\rangle\) (blue circles) which is fitted with a cosine function with free amplitude (red line). The error bars are computed assuming a shot noise limited error on the detected 4-fold coincidences. Using the fit parameters, the internal phase of the GHZ state is set to θ = 0[2π] when P = 52.81 mW. b The experimental (theoretical) 4-photon coincidence probability distribution measured in this configuration are reported in blue bars (dotted black bars). Along the horizontal arrow, the qubit states are ordered as {0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111}. c, d The real (top) and imaginary (bottom) parts of the reconstructed density matrix \(\rho =\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle \left\langle {{{{\rm{GHZ}}}}}_{4}\right\vert\) for the target (c, gray) are compared to the reconstruction from the experimental 4-photon tomography data using maximum likelihood estimation ρexp (d, green). The noise (±1e-9) in (c) arises from the numerical method (maximum likelihood estimation) and is orders of magnitude smaller than the noise arising from the imperfections of the experimental setup (±0.03) in ρexp.

Full size image

There are many tools available to detect entanglement and to estimate the fidelity of a multipartite system with minimal resources. Entanglement witnesses37,38, Bell-like inequalities39, or the so-called GHZ paradox33,40 all require only a few Pauli projective measurements to characterize the GHZ states. Here we choose the stabilizer witness for GHZ states \({{{{\mathcal{W}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\) (Methods) first introduced in ref. 41, for which a measured negative expectation value signals the presence of genuine multipartite entanglement, although with no indication about the state form. This witness requires only two projective measurements to detect entanglement, and to compute a lower bound of the fidelity of the generated state to our target \(\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle\), where \({{{{\mathcal{F}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\ge (1-\langle {{{{\mathcal{W}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\rangle )/2\). We found \(\langle {{{{\mathcal{W}}}}}_{\exp }\rangle =-0.65\pm 0.03\), which certifies that the generated state is entangled. The lower bound for the fidelity of the generated state to the target is \({{{{\mathcal{F}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\ge 0.82\pm 0.01\).

On-chip quantum-state tomography

The generated states can be fully characterized through the reconstruction of the density matrix via maximum likelihood estimation42 from a full quantum-state tomography. Because of the computational cost of quantum state tomography and of the necessity of long measurement time to collect suitable amounts of statistics, most previous on-chip entanglement generation protocols based on SPDC or SFWM sources15,43,44 use partial analysis of the state, such as partial state tomography, quantum compressed sensing or entanglement witnesses, to determine the state fidelity with respect to the target and to detect entanglement. Here the high single-photon rate of the QD source and the low insertion losses of the chip are the keys for increasing the experimental feasibility of a full quantum state tomography reconstruction of the density matrix of the 4-qubit state.

To fully reconstruct the 16 × 16 density matrix, 34 = 81 projective measurements, corresponding to all possible combinations of (σx, σy, σz) among the four qubits, are necessary. The density matrix is determined by using a maximum likelihood estimation to restrict the numerical approximation to physical states. The result is shown in Fig. 2d. From the experimental density matrix \({\rho }_{\exp }\) we calculated the fidelity \({{{{\mathcal{F}}}}}_{{{{{\rm{GHZ}}}}}_{4}}=\left\langle {{{{\rm{GHZ}}}}}_{4}\right\vert {\rho }_{exp}\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle =0.860\pm 0.004\) and the state purity \({{{{\mathcal{P}}}}}_{{{{{\rm{GHZ}}}}}_{4}}=Tr\{{\rho }_{exp}^{2}\}=0.763\pm 0.006\) can be retrieved. Our four-photon results overcome the state-of-the-art in terms of fidelity and purity for integrated implementations of GHZ states. Previous record values demonstrated in ref. 16 showed fidelity of 0.792 ± 0.012 for a four-photon GHZ state.

In what follows we investigate all the sources of noise in our system to analyse quantitatively what is limiting our values of fidelity and purity. In order to explore the effect of each experimental imperfection, we use a phenomenological model (Supplementary Note 4) based on the measured characteristics of the experimental setup to perform numerical simulations of the experiment45. The model accounts for (i) the imperfections of the single-photon source, namely the imperfect single-photon purity and indistinguishability of the input state made of four simultaneous photons, (ii) the imperfections of the preparation of the GHZ states, namely the imperfect directional couplers and initialization of the internal phase θ in the preparation stage (see Fig. 1), and (iii) the imperfections of the projective measurements, implemented by the MZIs, and detectors experimentally dominated by unbalanced detection efficiencies, modeled by imperfect projective measurements. Each imperfection is studied independently to uncover the main source of noise in the system. The results of the numerical simulations and the corresponding values of fidelity and purity are shown in Table 1.

Table 1 Numerical simulation of the fidelity and the purity of a 4-qubit GHZ state computed from the reconstruction of the density matrix with maximum likelihood estimation45
Full size table

The imperfections of the single photon source, namely the multiphoton terms and the partial distinguishability of the 4-photon input state, limit the achievable values of fidelity and purity. The multiphoton component g(2)(0) of the single-photon stream, measured independently in a Hanbury-Brown and Twiss setup, is g(2)(0) = 0.005 ± 0.001. The indistinguishability of two subsequent photons (12.3 ns time delay) measured with a Hong-Ou-Mandel (HOM) interferometer46 right at the output of the source is Ms = 0.962 ± 0.02 (see Supplementary Note 2). The indistinguishability of the 4-photon input state is limited by long-term fluctuations of the emitter environment (electrical and magnetic noise) when using the time-to-spatial demultiplexing scheme that synchronizes photons up to 500 ns apart (see setup in Supplementary Note 2). The indistinguishability of long-delay (500 ns time delay) photons is measured through the demultiplexer and the chip used as multiple HOM interferometers (Supplementary Note 2). We measure a 2-photon indistinguishability in the range 0.88 ± 0.01 < Ms < 0.92 ± 0.01, depending on the actual photon delays. The indistinguishability of the photons is degraded by the imperfect temporal overlap and imperfect polarization control of the photons at the output of the demultiplexer. It is also affected by fabrication imperfections of the optical circuit. We use all the accessible pairwise indistinguishabilities (see Supplementary Note 2) as inputs for the model. All the imperfections from the chip input to the detectors are thus taken into account twice, which explains why our phenomenological model underestimates the fidelity and purity when all the sources of noise are taken into account (see Supplementary Note 4).

Causal inequality for GHZ state certification

We further certify the presence of non-classical correlations within the generated state, by adopting an approach requiring fewer measurements than the full quantum state tomography and minimal assumptions on the experimental apparatus, i.e., in a semi device-independent fashion.

We use Eq. (2) as a special case of generic Bell Inequalities for self-testing graph states that can be found in47. Under the assumptions detailed and justified in Supplementary Note 5, a violation of Eq. (2) guarantees the presence of non-classical correlations among the parties. Like for a two-partite Bell measurement, the orthogonal measurement bases \(({M}_{0}^{(i)},{M}_{1}^{(i)})\) for each of the four qubits i ∈ {1,.. , 4} have been set to obtain the highest violation of Eq. (2) for the target state \(\left\vert {{{{\rm{GHZ}}}}}_{4}\right\rangle\), i.e., \(6\sqrt{2}=8.48\). Each of these 2-qubit Pauli projectors are defined in the Methods section. A maximal quantum violation self-tests that the generated state has the form of the target state48,49.

$$\begin{array}{l}{{{{\mathcal{I}}}}}^{2}=\mathop{\sum }\limits_{i=2}^{4}\left\langle {M}_{0}^{(1)}{M}_{1}^{(i)}\right\rangle -\mathop{\sum }\limits_{i=2}^{4}\left\langle {M}_{1}^{(1)}{M}_{1}^{(i)}\right\rangle +3\left\langle {M}_{0}^{(1)}{M}_{0}^{(2)}{M}_{0}^{(3)}{M}_{0}^{(4)}\right\rangle\\\qquad\; +\,3\left\langle {M}_{1}^{(1)}{M}_{0}^{(2)}{M}_{0}^{(3)}{M}_{0}^{(4)}\right\rangle \le 6\end{array}$$
(2)

We compute the expectation values of the left hand side of Eq. (2) (see Methods). Abiding Eq. (2) would mean the measured probabilities could be compatible with a local hidden variable model, according to the directed acyclic graph in Fig. 3a50. On the contrary, a violation of Eq. (2) certifies the presence of non-classical correlations among the parties. In our case, the largest experimental estimate of \({{{{\mathcal{I}}}}}^{2}\) is 7.49 ± 0.04 > 6, which violates the classical bound described in Eq. (2) by 39 standard deviations.

Fig. 3: Semi-device independent certification of the GHZ4 state.
figure 3

a Causal structure. In the DAG shown here, there are three different kinds of nodes: Λ is a hidden variable (blue box), (M0, M1) are measurement settings (yellow boxes) and each party is associated with a variable (i) outputting measurement outcomes. b Violation of the Bell-like inequality characterizing 4-partite GHZ states. The violation of the Bell-like inequality certifies the presence of non-classical correlations. We study the dependence of the entanglement of the GHZ state on the dominant source of noise, i.e., the minimal pairwise 2-photon indistinguishability. A half-wave plate is used to rotate the polarization of photon C and make it distinguishable from A, B, and D. The measured 2-photon mean wavepacket overlap (HOM) is shown in the insets for 2 datapoints. The experimental data (black squares) and simulation (red circles) demonstrates a good numerical match. Error bars for the violation of the inequality, referring to the 95% confidence interval, are obtained from error propagation assuming a shot noise limited error on the total number of 4-fold coincidences. Error bars for the minimal HOM correspond to the standard deviation of the measured 2-photon interference visibility distribution measured between each combination of binary measurements. The violation of the Bell-like inequality reaches a maximal value of \({{{{\mathcal{I}}}}}^{2}=7.49\pm 0.04\) when all photon have the highest pairwise indistinguishability, which certifies non-classical correlations and non bi-separability within 39 standard deviations.

Full size image

Furthermore, we address the robustness of our inequality violation with respect to the experimental noise. Since we have identified partial distinguishability as the main source of noise in our system, we vary in a controlled way the indistinguishability among the parties, i.e., make one of the four photons distinguishable in the polarization degree of freedom using a half-wave plate, to gauge how robust the entanglement is with respect to this issue. In Fig. 3b, we report the measured values for \({{{{\mathcal{I}}}}}^{2}\) while increasing the photon distinguishability, which we calibrated with independent measurements (Supplementary Note 2). Our setup can tolerate a substantial amount of distinguishability before inequality \({{{{\mathcal{I}}}}}^{2}\) is not violated anymore. In Fig. 3b we observe a good agreement between experimental data and simulations for different levels of noise, which reveals that our model can faithfully describe the generated state for a wide range of input parameters.

Quantum secret sharing

We now examine the suitability of our approach to implement “Quantum secret sharing” (QSS)—a protocol presented in 1999 by ref. 34. This protocol, as many others in quantum communications, only requires projective measurements by each party, and it is therefore compatible with post-selected entangled states. QSS considers the practical case of a regulator who wants to share a secret string of random bits with three interlocutors, in such a way that they can access the secret message only if they cooperate all together. In this protocol, the regulator prepares a string of 4-qubits in a state of the form of Eq. (1), keeps one qubit and distributes the three others to three parties. All four parties then randomly choose a basis for measuring the state of their qubit: σx or σy. The sifted key is extracted, on average with a 50% success probability, after public basis sharing (see Supplementary Note 6 for more details). Experimental implementations of QSS protocols exploiting multipartite entangled states of light51,52, including 3- and 4-photon GHZ states53,54 have already been reported, relying on bulk optics.

We performed a proof-of-principle implementation of this QSS protocol by generating the 4-qubit GHZ state with our chip and by exploiting the reconfigurable MZIs to perform the required projective measurements. Each party measures its share of the 4-qubit GHZ state by randomly selecting a measurement basis, and by recording the measurement outcome in the raw key when the first 4-photon coincidence event occurs. This procedure is repeated until the target length for the raw key has been reached. The key sifting is then performed by discarding the raw bits that correspond to non-valid basis choices. The raw bit generation rate we obtained is about 0.5 Hz. This rate incorporates the dwell time to reach stable settings (~100 ms) for the randomly chosen projective measurements.

We evaluate the total number of errors by calculating the quantum bit error rate (QBER) on the sifted key. An uninterrupted run with optimized pairwise indistinguishability between all photons provided a QBER of 10.87% ± 0.01, which guarantees a secure communication as it is below the required threshold of 11%55, with a raw length of 4060 bits, and a sifted length of 1978 bits.

Discussion

In this work we demonstrated the generation of 4-photon multipartite GHZ states integrating an on-demand solid-state QD-based SPS with a reconfigurable glass photonic chip. We achieved a post-selected 4-fold coincidence rate of 0.5 Hz with a pump rate of 79 MHz, which allowed us to perform full quantum state tomography, with a fidelity of 86% to the target state. A 4-photon coincidence rate of 10 Hz was reached removing one stage of spectral filtering on the single photon source with a limited effect (+0.007 on g(2)(0) and −0.05 on Ms, see Supplementary Note 2). The combination of high-fidelity and high rate, as well as the overall platform stability —stable enough for highly demanding measurements such as full quantum state tomography—paves the way to the use of this platform for entanglement-based quantum protocols.

Our systematic analysis and numerical modeling shows that, despite state of the art performances of the source, the effective overall indistinguishability of the photons is the main limiting factor to the ideal fidelity. We thus identify many handles to further improve these results. Our observations indeed indicate that the effective indistinguishability of the QD photons at long delays is limited by the stability of the voltage source used to operate the QD, which can be mitigated using electrical filters placed close to the electrical contacts of the gate-voltage of the single-photon source. More precise temporal overlap of the photons and better polarization control at the input of the chip would also increase the net photon overlap. In the current demonstration, we have 50% insertion losses on the chip. This is not an intrinsic limit and it can be greatly reduced by future optimization of the writing process and of the substrate material composition. Finally, the operation rate can be brought up to at least 500 MHz thanks to the short photon profile. All these improvements would allow to significantly improve state fidelity and purity, and increase performances for applications, i.e., a higher bitrate and a lower QBER in the QSS protocol.

All together, these qualitative and quantitative results constitute an important milestone in the generation and use of high-dimensional quantum states. They prove that the integration of QD-based SPSs with glass chips for generation and manipulation of multipartite states is now mature and can lead to performances comparable to those achievable by state-of-the-art free space implementations. The on-demand nature of QD-based SPSs along with the integration of low-loss, stable, and re-configurable optical elements in a photonic glass chip put our platform in the front line for the development of practical photon-based quantum devices. The QD source used in our implementation has definite assets for real-world applications: the long-term stability enabled by the solid state cavity allows for long operation times, deterministic fabrication technique for many device implementations and high potential for integrability. Emission wavelength of QDs in the NIR spectral range is not optimal for long distance quantum communications, but can be converted to the telecom range via quantum frequency conversion devices56. The combination of these sources with laser-written circuits will be a key feature for both quantum communications and distributed quantum computing, given the excellent matching of our waveguides with optical fibers. The latter also allows for a modular architecture, which is a powerful route to scalability and enables to use the best available sources and detectors in a plug-and-play approach.

Recent works have shown the ability to generate linear cluster state at high rate using an entangling-gate in a fiber loop57, or through spin-photon entanglement11, harnessing a similar QD-based single-photon source. Generating multipartite entanglement on chip, as demonstrated here, will be key to obtain the 2D cluster states required for measurement-based quantum computation.

Methods

Single-photon source

The bright SPS consists of a single InAs QD deterministically embedded in the center of a micropillar18. The sample was fabricated using the in-situ fabrication technology58,59 from a wafer grown by molecular beam epitaxy composed of a λ-cavity and two distributed Bragg reflectors (DBR) made of GaAs/Al0.95Ga0.05As λ/4 layers with 36 (18) pairs for the bottom (top). The top (bottom) DBR is gradually p(n)-doped and electrically contacted. The resulting p-i-n diode is driven in the reversed bias regime to reduce the charge noise60 and to tune the QD in resonance with the microcavity. The resonance of the QD with the cavity mode at λQD = 928 nm is actively stabilized in real time with a feedback loop on the total detected single-photons countrate. The sample is placed in a closed-loop cryostat operating at 5 K. The longitudinal-acoustic (LA) phonon-assisted excitation61 is provided by a shaped Ti:Sa laser at λexcitation = 927.4 nm, generating ~15 ps pulses with a repetition rate of 79 MHz. The (polarized) first-lens brightness, defined as the (polarized) single-photon countrate before the first optical element computed from the loss-budget presented in Supplementary Note 2 is (βFL = 38%) βFL = 50%, leading to a detected countrate of 12.3 MHz, corresponding to an estimated countrate of 18.9 MHz taking into account the 65% efficiency of the SNSPD. To improve the single-photon purity and indistinguishability of the source a narrow optical filter (FWHMfilter = 4 × FWHMphoton, T = 60%) is added to the laser filtering module (Supplementary Note 2). With this additional spectral filter the detected single-photon countrate is 7.4 MHz.

The single-photon stream is split into four spatial modes using an acousto-optic based time-to-spatial demultiplexer. The time of arrival of each photon at the input of the optical circuit is synchronized with fibered delays (0 ns, 180 ns, 360 ns, 540 ns). The polarization of each output is actively controlled with motorized paddles for 5 min every 1 h, to account for the temperature instability in the laboratory.

Projectors

The projectors \({M}_{0}^{(i)}\) and \({M}_{1}^{(i)}\) used in the definition of the operator \(\hat{\Theta }\) for the characterization of the phase θ, and in the Bell-like inequality expressed by Eq. (2) are: \({M}_{0}^{(1)}=\frac{{\sigma }_{x}+{\sigma }_{z}}{\sqrt{2}}\), \({M}_{1}^{(1)}=\frac{{\sigma }_{x}-{\sigma }_{z}}{\sqrt{2}}\), \({M}_{0}^{(3)}={\sigma }_{x}\), \({M}_{1}^{(3)}={\sigma }_{z}\), \({M}_{0}^{(2)}={M}_{0}^{(4)}=-{\sigma }_{x}\) and \({M}_{1}^{(2)}={M}_{1}^{(4)}=-{\sigma }_{z}\).

Expectation values

For a given 4-qubit projector \(\hat{E}\), the expectation value is computed as \(\langle \hat{E}\rangle =\mathop{\sum }\nolimits_{i = 1}^{16}{p}_{i}{{{{\mathcal{E}}}}}_{i}\), where pi is the probability of detecting the 4-qubit output state i associated to the measured normalized 4-photon coincidence rate of each possible output state and \({{{{\mathcal{E}}}}}_{i}=\pm 1\) is the product of the individual outcomes where +1 is associated with the detection of \(\left\vert 0\right\rangle\) and -1 is associated with \(\left\vert 1\right\rangle\). Note that whenever we have \({\mathbb{1}}\) in an expectation value for a qubit then we always record +1 (irrespective of which detector have clicked) which amounts to trace out the corresponding qubit.

Stabilizer witness

The stabilizer witness \({{{{\mathcal{W}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\)37 can be computed from the generating operators \({g}_{1}^{({{{{\rm{GHZ}}}}}_{4})}={\sigma }_{x}\otimes {\sigma }_{x}\otimes {\sigma }_{x}\otimes {\sigma }_{x}={\sigma }_{x}^{\otimes 4}\) where ⊗ is the Kronecker product of the Pauli matrices, and \({g}_{k}^{({{{{\rm{GHZ}}}}}_{4})}=-{\sigma }_{z}^{(k-1)}\otimes {\sigma }_{z}^{(k)}\) for k = 2, 3, 4 (the identity operator \({\mathbb{1}}\) has been omitted for two of the parties not involved) as

$$\frac{{{{{\mathcal{W}}}}}_{{{{{\rm{GHZ}}}}}_{4}}}{3}={\mathbb{1}}-\frac{2}{3}\left[\frac{{g}_{1}^{({{{{\rm{GHZ}}}}}_{4})}+{\mathbb{1}}}{2}+\mathop{\prod }\limits_{k=2}^{4}\frac{{g}_{k}^{({{{{\rm{GHZ}}}}}_{4})}+{\mathbb{1}}}{2}\right].$$
(3)

To compute these expectation values, we need to perform only two projective measurements, namely \({\sigma }_{x}^{\otimes 4}\) and \({\sigma }_{z}^{\otimes 4}\). This witness allows to give a lower bound on the fidelity via \({{{{\mathcal{F}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\ge (1-\langle {{{{\mathcal{W}}}}}_{{{{{\rm{GHZ}}}}}_{4}}\rangle )/2\). A measured negative expectation value signals the presence of genuine 4-partite entanglement. Indeed, the expectation value of this witness takes its minimum value, i.e., -1, when the state under scrutiny is a 4-qubit GHZ state, while it is larger for any other state. Since in proximity of the target state there are only state displaying genuine multipartite entanglement, the threshold of such a witness is chosen so that only this kind of entanglement is detected. It is also noteworthy that the witness in Eq. (3) is robust to the following white noise model:

$$\rho ={p}_{N}\frac{{\mathbb{I}}}{4}+(1-{p}_{N})\left\vert GH{Z}_{4}\right\rangle \left\langle GH{Z}_{4}\right\vert$$
(4)

up to a \({p}_{N} \,<\, \frac{1}{3-{2}^{(2-n)}}\), which for n = 4 amounts to ~0.36.