Introduction

Prediction is of prime importance in natural disaster management; consequently, extreme flood prediction helps experts minimize its deleterious effects. During recent years hydrological and statistical communities developed extreme flood prediction approaches (Brigode et al. 2014). Based on their probability distributions, these methods calculate the average return period to extreme streamflows based on their probability distributions. In classical flood frequency analysis (FFA) and using extreme value theory, by fitting an estimated probability distribution to the observed streamflow values, the probability distribution of the maximum discharges or extreme floods is defined (Fréchet 1927; Gumbel 1958; Khaleghi and Varvani 2018; Singh and Strupczewski 2002; Merz and Bloschl 2008). The FFA methods have some limitations, the main disadvantage of these models is that most do not allow the generation of temperature time series, which is essential in predicting how snow melts. Moreover, most of them work only in a daily time step which makes this method unsuitable for small and fast responding watersheds. The FFA approach also has the problem of the statistical period of the flood data being insufficient in some cases. Further, due to climate changes or anthropogenic activities may not have suitable stationary.

Other models such as HEC-HMS use parameters such as land use/land cover, soil permeability, and other hydrological conditions to predict the volume and peak of floods due to the lack of adequate and appropriate hydrometric data (Gholzom and Gholami 2012; Varvani and Khaleghi 2018). The curve number (CN) method is one of the widely used approaches in this category for estimating direct runoff from rainfall events. Despite its popularity and ease of use, event-based models have several limitations. Reliance on a single parameter (CN), assuming a constant initial abstraction ratio and sensitivity to antecedent moisture conditions (AMC) can lead to significant uncertainty in runoff prediction (Varvani and Khaleghi 2018; Theodosopoulou et al. 2022).

Rainfall-runoff models have been widely used in extreme flood prediction and are more important than statistical methods, especially for predicting floods with high return periods (Lawrence et al. 2014; Gholami and Sahour 2021). In addition, stochastic prediction approaches have made their appearance during the last two decades (Calver and Lamb 1995; Franchiniet al. 1996; Cameron et al. 1999; Blazkova and Beven 2002; Sivapalan et al. 2005a). These methods are defined from a statistically based flood sample analysis predicted by rainfall-runoff models, which are linked to a probabilistic precipitation model that can be developed in the context of a continuous prediction or the form of a single prediction or a series of event-based predictions. In recent years, with the strengthening of the computing power of computers to predict precipitation as input to models, continuous methods have been much more advanced than event-based methods (Boughton and Droop 2003; Pathiraja et al. 2012). A variety of observed rainfall features can be replicated by continuous stochastic rainfall methods, according to different studies (e.g.,, Rodríguez-Iturbe et al. 1987; Cowpertwait 1995; Schmitt et al. 1998; Arnaud and Lavabre 1999; Willems 1999; Olsson and Burlando 2002; Bernarda et al. 2007; Lennartsson et al. 2008; Papalexiou et al. 2011). Continuous prediction methods are limited by the complexity of stochastic rainfall patterns, according to Rogger et al. (2012). Watershed saturation hazards are explained by the rainfall-runoff model based on the sophistication of the extreme streamflow prediction exercise (Verhoest et al. 2010; Pathiraja et al. 2012; Li et al. 2013; Gholami et al. 2021). Rainfall-runoff models can predict flood events using the marked rainfall events. These approaches must be able to reproduce the three following factors that are important in flood generation: (a) the stochastic rainfall models specify rainfall hazards, (b) hydro-climatological records describe the watershed saturation hazard, and (c) rainfall-runoff models describe the rainfall-runoff transformation (Gholami et al. 2009; Brigode et al. 2014). The entire complex steps for extreme flood prediction described in the preceding sections are presented by a creative method called SCHADEX (Simulation Climato-Hydrologique pour l’Appréciation des Débits EXtrêmes). Paquet et al. (2013), and Garavaglia (2011) proposed the SCHADEX as a semi-continuous stochastic prediction method that predicts rainfall hazards on an event-basis while predicting watershed saturation hazards through continuous rainfall-runoff modeling. Based on a daily and hourly assessment of twenty rainfall-runoff models, the SCHADEX approach structure was used to develop a lumped conceptual rainfall-runoff model (Mathevet 2005; Andreassian et al. 2006). In their impressive study, which was tested on a sample of 313 watersheds, the results showed that MORDOR's rainfall-runoff model structure is more efficient, robust, and accurate (Paquet et al. 2013). Different studies were performed using the lumped MORDOR rainfall-runoff model for the SCHADEX approach (Garavaglia et al. 2012; Penot et al. 2014; Valent et al. 2014; Evin et al. 2016; Valent and Paquet 2017). The new model aims to assess the impact of model equations and spatial separation on streamflow prediction, snowpack representation, and evapotranspiration prediction. However, there is little evidence that this approach is more accurate than the classic one in terms of the various streamflow signatures, evapotranspiration, and snow predictions (Duan et al. 2006; Hollander et al. 2009; Garavaglia et al. 2017).

Climate variability, especially its changes during the year, strongly affects the frequency of floods in two ways: directly through seasonal changes in the characteristics of storm events and indirectly through seasonal precipitation and evapotranspiration on the previous humidity conditions of the basin (Sivapalan et al. 2005a). Seasonality of storm specifications and AMC on flood frequency are of prime importance, these effects, have never been evaluated in any of the flood frequency models in the past studies. While the continuous modeling that will be used in this research has this advantage over the event based models in that the rainfall-runoff model continuously calculates the AMC. Mathematical models recognizing seasonality must be the links between long-term water balance models and derived flood frequency models (Sivapalan et al. 2005b). In the mountainous watersheds, snowmelt is a very important factor in flood occurrence and the model used in the prediction should have a suitable solution for its participation in peak streamflow. In event based methods, especially in the areas where accumulation and melting are quite different seasons or spatially varying in watershed topography, it can be a particular challenge. Spatial discretization is a component of the semi-distributed hydrological model incorporated in this research. Based on elevation zones, this discretization is both efficient and parsimonious for mountainous hydrology.

In this study, a new approach is proposed to predict the hydro-climatic process in mountainous watersheds. The proposed method does not only consider climate variability but also would be more accurate rather than conventional methods in extreme flood prediction. None of the studies employed a semi-distributed rainfall-runoff model and seasonality of water balance characteristics altogether. The goal of this study is to model extreme floods using hydro-climatic data in mountainous watersheds.

Materials and methods

Study area

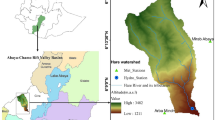
In this study, the Bakhtiary watershed was selected for the hydro-climatic method for extreme flood prediction. This watershed is located in the southwest of Iran at the eastern longitude of 48° 15´ to 50° 20´ and the northern latitude of 32° 30´ to 33° 30 (Fig. 1). Iran’s Meteorology Organization (IMO) and Iran Water Resources Management Organization (IWMO) are two governmental organization that has responsibility for measuring, recording and publishing rainfall, discharge, temperature and other climatologic and hydrologic data in Iran. For areal precipitation calculation, daily data of some rain gauge stations inside and outside of the Bakhtiary watershed was used, and eight stations belong to IWMO and eight stations belong to IRIMO (Fig. 1). The study watershed has a cold mountain climate. The predominant shape of precipitation is rain, but snowfall is also observed. Further, the height of the watershed area varies between 394 and 4049 m.

Fig. 1
figure 1

A Location of the study watreshed in Iran, B Location of the study river, meteorological stations, and hydrometric station

Full size image

Model input data

Air temperature (evaporation), precipitation, soil moisture, and streamflow are the main variables in hydrology that describe the hydrological function of watersheds. Reliable time series are necessary for research and operational applications, such as water resource management, flood or drought predetermination, flow forecasts, and climate variability analysis (Tencaliec et al. 2016). The term that is used to data quality-check and/or fill the gap is data screening, which is used for precipitation, temperature, and streamflow datasets and represents a great challenge in hydrology and geosciences in general.

Availability of records in the same base time for two different resources of data is necessary for areal rainfall computations. In other words, some years have missing data; therefore, to reconstruct precipitation data, a statistical method was used. The nearest and more completed time series rain gauges inside and close to the case study were acceptable for this purpose. Reconstructing missed rainfall data according to multilinear regressions (Tencaliec et al. 2016) based on neighboring stations, led to the creation of the same base time series for rainfall data. Thiessen polygon method was used to compute an aerial averaged precipitation that is estimated using the location of rain gauge stations (Table 1). For this purpose, 16 reconstructed rain stations were taken into account; consequently (Fig. 1), concerning the weight of each station that participated in the calculation of areal precipitation. Finally, six rain gauges participate in areal precipitation computation (Table 2).

Table 1 IWMO and IRIMO rain gauge stations inside and around Bakhtiary catchment
Full size table
Table 2 Selected rain gauges and weights for predicting the areal precipitation
Full size table

Temperature is of prime importance in this study. The source station for temperature that has adequate data (1976–2013) is the Tange-Panj station. Using means of the regression model coefficients, all odd daily data for years 2000, 2004, 2005, 2006, and 2009 missing temperature dates were reconstructed, finally, to verify these processes and the double homogeneity test, the useful approach proposed by Musy et al. (2005) was used. Ellipse de Bois is an approach that can lead to reducing the effect of cumulative residuals in the regression method.

Tange-panj-e-Bakhtiary station is a hydrometric station that is located in the watershed outlet, therefore, to evaluate discharge data accuracy, two stations (Sepiddasht and Talezang stations) around this station were selected as a base station for data homogeny test. These two stations are located up-stream and down-stream of Tange-panj station. To identify the odd or biased year, the cumulative residuals for each base station versus Tange-panj were calculated, and then confidence interval ellipses around cumulative residuals via parameters calculations were drawn. Fortunately, there are no outlier data in stations and Tange-panj, for Sepiddasht and Talezang stations. To complete the discharge data series for modeling, reconstruct missing data by regression model according to the nearest stations around Tange-panj for some dates used.

Hydro-climatic modeling of extreme flood occurrence

Extreme hydrological events have been studied a lot in recent decades, but due to the spatial changes of precipitation processes that cause streamflow, establishing a clear view of how streamflow has changed and its changes in the future are not easily predictable (Wang et al. 2008). There are different statistical tools for assessing changes in extremes (Şen et al. 2017), Mann–Kendall trend test (Mann 1945; Kendall 1948), which is a rank-based non-parametric method, is applied for maximum yearly discharges in the present study. Because the estimated p value is lower than the significance level (p value > 0.05), one should reject the null hypothesis H0, and accept the alternative hypothesis Ha (There is a trend in the series). The risk of rejecting the null hypothesis H0 while it is true is lower than 1.52%. The continuity correction was performed. Ties were detected in the used data and the appropriate corrections were used and Sen's slope is equal to 7.

The non-parametric Pettitt’s test method (Pettitt 1979) was used to define the point of change in time series that separates the whole period into the disturbed and undisturbed periods. Pettit’s test can be used to identify whether two selected data samples belong to an equivalent population supported by the mean of your time series and therefore the Mann–Whitney statistic. Therefore, Pettit’s test was used for the time series of flow discharge for the Bakhtiary watershed. As the computed p value (0.046) is lower than the significance level alpha = 0.05, one should reject the null hypothesis H0, and accept the alternative hypothesis Ha (There is a date at which there is a change within the data). The risk of rejecting the null hypothesis H0 while it is true is lower than 4.62 percent. The terms “natural” and “disturbed” periods were defended for discharge time series (Kakaei et al. 2019). Generally, changes in land use and crop patterns might have caused the pattern in discharge time series, as well as abstraction from surface and groundwater resources in watersheds. In this study, the period 1951–1976 was introduced as a disturbed period, and 1976–2013 was defined as a natural period. Consequently, a natural period calibration and validation should be performed on the hydrological model. Finally, the following methods were used to predict extreme flows.

The SCHADEX method

SCHADEX is a probabilistic method that uses time series of precipitation, discharge data, and air temperature, as well as flood hydrographs for predicting semi-continuous extreme floods. The precipitation hazard and the watershed saturation hazards are two assumed natural hazards and the general idea behind SCHADEX for extreme floods stochastic prediction framework based on a rainfall-runoff model. A daily time step was used in this stochastic prediction framework, although sub-daily applications were also possible. A semi-distributed rainfall-runoff model is used, meaning input values should represent area averages based on the range of elevations of the watershed. Event basis prediction for areal rainfall hazard and continuous rainfall run-off modeling for modeling watershed saturation hazard used in the SCHADEX approach, imply semi-continuous modeling in the SCHADEX stochastic prediction framework. Simulating rainfall events rather than a continuous rainfall series reduces the complexity of probabilistic modeling of dry and wet sub-periods. The rainfall events are considered in three parts, the central precipitation and the two adjacent precipitations, which are smaller than the central one. The rainfall event is based on the correlations between rainfall and peak flows (Paquet et al. 2013).

The peak-to-volume ratio is employed to convert the daily discharge distribution (QJ) into a peak discharge distribution (QX), by transferring the cumulative distribution function (CDF) of daily discharges to a CDF of peak discharge: QX(T) = K.QJ(T), where T is the return period (Tr). The peak-to-volume ratio is often estimated as the mean peak-to-volume ratio K = E [QX(i)/QJ(i)] of a selection of the observed discharges during major floods.

In the study watershed, 26 hydrographs were evaluated. The maximum discharge rates of the selected hydrographs were between 16.6 and 1143 cubic meters per second. The mean-centered peak-to-volume ratio K is 1.35.

Probabilistic rainfall model

According to much of the hydrological literature of recent years, a critical step in predicting extreme flood quantiles is to treat the exact prediction of extreme rainfall quantiles. Based on the theory of extreme values, one of many solutions is the use of an asymptotic model to describe the stochastic behavior of extreme value processes. Independence, stationarity, and homogeneity are three hypotheses for modeling extremes based on standard methodology. Garavaglia et al. (2010a, b) introduced the concept of the multi-exponential weather patterns (MEWP) distribution as a way to probabilistically describe central rainfall. This concept served as the foundation for Paquet et al. (2013) to develop the SCHADEX method. For the definition of a MEWP model, we have to classify a WP at the regional scale in advance. To model each sub-sample under consideration, an exponential law is used. The global distribution of MEWPs encompasses various exponential laws that intertwine to form a comprehensive framework. The frequency of each WP central rainfall observation is the basis for weighting this compound. The formulation of the MEPM distribution for a specific season is provided in Eqs. (1) and (2):

$${{\text{F}}}^{{\text{i}}}\left({\text{CR}}\right)=\sum_{{\text{j}}=1}^{{{\text{n}}}_{{\text{wp}}}}{{\text{F}}}_{{\text{j}}}^{{\text{i}}}\left({\text{CR}}\right)*{{\text{p}}}_{{\text{j}}}^{{\text{i}}}$$
(1)
$${{\text{F}}}^{{\text{i}}}\left({\text{CR}}\right)=\sum_{{\text{j}}=1}^{{{\text{n}}}_{{\text{wp}}}}\left[1-{\text{exp}}(-\frac{{\text{CR}}-{{\text{u}}}_{{\text{j}}}^{{\text{i}}}}{{\uplambda }_{{\text{j}}}^{{\text{i}}}})\right]*{{\text{p}}}_{{\text{j}}}^{{\text{i}}} (2)$$

where i is the selected season, CR is the observed central rainfall, j is the studied WP, p is the CR event probability of occurrence of the WP, nWP is the number of WP, F is the marginal distribution, and u is a threshold for selecting heavy rainfall observation. The SCHADEX framework does not utilize the complete rainfall data series to emphasize the MEWP distributions. Instead, we employ CR to select the central rainfall sample, which allows for a peak-over-threshold (POT) sampling approach for the observed daily rainfall series. The relation between MEWP probability and return period is given in Eq. (3):

$${\text{T}}\left({\text{CR}}\right)=\frac{1}{1-{\text{F}}{({\text{CR}})}^{\frac{{\text{n}}}{{\text{N}}}}}$$
(3)

where T is the return period in years, n is the size of the precipitation observation sub-sample under consideration, and N is the number of years in the CR series under consideration. Using a bottom-up approach suggested by (Brigode et al. 2013), four typical atmospheric circulations for Iran have been identified. These weather patterns according to meteorological genesis produce distinct weather patterns that align with Iran's climatology. This enables the division of seasonal rainfall records into more uniform sub-samples. Since 1951, each day has been linked to a specific WP. It is crucial to consider seasonality when creating rainfall probabilistic models, as the relevant seasons need to be identified and defined.

Rainfall-runoff model

To utilize the SCHADEX method effectively, it becomes necessary to have a rainfall-runoff model that serves two main purposes. Firstly, it helps to assess the saturation hazard in the study watershed. Secondly, it facilitates the conversion of various "extreme synthetic rainfall events" into extreme floods. The MORDOR-SD (Garavaglia et al. 2017) model is an improved version of the MORDOR (Garçon 1996) model, incorporating a spatial discretization scheme. This daily semi-distributed continuous model offers enhanced capabilities for analysis and modeling. The elevation zone approach is the basis of this discretization, therefore, meteorological forcing spatial variability is described by their orographic gradient. In this approach, assume that spatial variability for temperature and precipitation is mainly driven by elevation. The majority of model variables are computed for each elevation zone, exception for groundwater and outflow content. These two variables are evaluated on a global scale, encompassing the entire watershed. The complete hydrological modeling scheme is described in detail in Garavaglia et al. (2017). The MORDOR-SD model was calibrated for the Bakhtiary watershed based on a genetic algorithm Wang (1991) using a multi-criteria composite objective function that is minimized during calibration, it is expressed as (Eq. 4):

$${\text{OF}}=\left(1-{{\text{KGE}}}_{{\text{Q}}}\right)+\left(1-{{\text{KGE}}}_{{\text{Qsea}}}\right)+(1-{{\text{KGE}}}_{{\text{FDC}}})$$
(4)

where KGE is the Kling–Gupta efficiency (Gupta et al. 2009), which is made up of three elements: correlation, variance bias, and mean bias. The triple focus on time series (KGEQ), seasonal streamflow (KGEQsea) and flow duration curve (KGEFDC) can correctly identify the various components of the model. The model was evaluated using the split-sample test as recommended by Klemes (1986) and Gharari et al. (2013). For the Bakhtiary watershed, we divided the complete data into two periods (P1 = 1976–1984 and P2 = 1984–2012). Initially, the models were calibrated during period P1 and then proceeded to validate them during period P2. The first year of the prediction was assumed to be the warm-up period. The function of periods was later swapped, with P2 being used for calibration and P1 for validation.

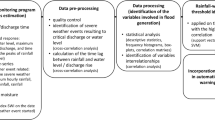
Model performance was evaluated using the classical Nash–Sutcliffe efficiency (NSE). The final component of the prediction evaluates the ability of the model to accurately predict the maximum daily flows. The calculated NSE value for the maximum daily flows induced by the observed centered rainfall event was 0.97. Represents inter-annual flow regimes and CDFs calculated for observed and predicted maximum daily flows. A flowchart of rainfall-runoff modeling steps by the MORDOR-SD method is given in Fig. 2.

Fig. 2
figure 2

Overview of MORDOR SD model components and fluxes (left), hypsometric curve, and elevation zones for Bakhtiary watershed

Full size image

Results

To accurately assess the practical applicability of the stochastic semi-continuous prediction method, it is essential to compare it with conventional methods. Therefore, four various models were used for extreme discharge prediction. A residual plot for raw temperature data on the surface of the Bakhtiary watershed is given in Fig. 3. The confidence interval (95%) around the predicted value is shown in Fig. 4. Further, the "Ellipse de Bois" schematic view for checking the homogeneity test was performed. The results of the Tange-panj versus surface temperature of NCEP/NCAR (National Centers for Environmental Prediction/National Center for Atmospheric Research) reanalysis database (1976–2013) were shown in Fig. 5A. Further, Tange-panj-e-Bakhtiary VS Sepiddashtzaz (1962–2007), and Tange-panj-e-Bakhtiary VS Talezang (1962–2007) were shown in Figs. 5B, C

Fig. 3
figure 3

Residual plot for raw temperature data, Bakhtiary VS NCEP

Full size image
Fig. 4
figure 4

Confidence Interval 95% limit lines around predicted value for Bakhtiary Versus T2M-NCEP

Full size image
Fig. 5
figure 5

"Ellipse de Bois" schematic view for checking homogeneity test, A Tange-panj versus surface temperature of NCEP/NCAR reanalysis database (1976–2013), B Tange-panj-e-Bakhtiary VS Sepiddashtzaz (1962–2007), and C Tange-panj-e-Bakhtiary VS Talezang (1962–2007)

Full size image

The Bakhtiary Watershed is divided into four distinct seasons, spring, summer, autumn, and winter. These seasons are categorized as follows concerning to the distribution of the MEWP: (a) February, March, October, and November, (b) April and May, (c) June to September, and (d) January and December. The period from January to December presents the greatest risk of heavy rainfall. Throughout the entire season, the MEWP distribution estimates that the daily rainfall for a 1000-year event is 226 mm. The resulting global MEWP model of central rainfall is shown from a CDF perspective. The model fits very well with the observed central rainfall and clearly states that there is no significant bias in the observed highest quantiles. Climatic and discharge data were analyzed. Mann–Kendall trend test and Pettit’s test were performed for maximum yearly discharge analysis in the hydrometric station and the results were given in Fig. 6. Moreover, Fig. 7 shows the MEWP distribution for February, March, October, and November central rainfall. One way to assess the effectiveness of a model is by comparing its predicted values to the actual observed values. In this case, Fig. 8 displays a comparison of the inter-annual flow regimes in the Bakhtiary watershed, showing both the observed and predicted values. Further, Fig. 9 shows the main components of the MORDOR-SD model in the one year of the prediction period.

Fig. 6
figure 6

A Mann–Kendall trend test, and B Pettit’s test for maximum yearly discharge analysis in the hydrometric station (mu1 is mean discharge of period 1, and mu2 is mean discharge of period 2)

Full size image
Fig. 7
figure 7

MEWP distribution and WP for February, March, October, and November central rainfall

Full size image
Fig. 8
figure 8

Comparison of the observed and predicted inter-annual flow regimes in Bakhtiary watershed

Full size image
Fig. 9
figure 9

Main components of model and various observed and predicted parameters (in1994-1995) by MORDOR-SD model

Full size image

CDFs for the maximum daily flows generated by the observed centered rainfalls were calculated and the results were shown in Fig. 10. A Comparison of CDFs calculated for the maximum daily flows generated by the observed centered rainfalls was performed. The SCHADEX method was used for predicting daily discharge and the model results were compared with the observed discharge values. Figure 11 shows the distribution of daily discharge (Q24) values based on the SCHADEX prediction. Further, hydrographs were selected for computing the peak-to-volume ratio. The scatter plot for the peak-to-volume ratio is given in Fig. 12. Furthermore, the CDF of predicted peak discharges and corresponding observations (QXc) is given in Fig. 13. The predicted 1000-year peak discharge is 9196 cubic meters per second. According to the results, the Nash–Sutcliffe and Kling-Gupta coefficients were 0.69 and 0.82 for the mean daily streamflow, 0.98 and 0.98 for the seasonal streamflow, 0.98 and 0.94 for the maximum discharges, and 0.57 and 0.78 for low flows, respectively. Then, the daily discharges in different return periods were estimated using the results of the MORDOR-SD model, considering the probability distribution function of the probabilistic model of central precipitation (MEWP), the probabilistic model of adjacent precipitation, and the probability distribution function of the previous precipitation.

Fig.10
figure 10

Comparison of CDFs calculated for the maximum daily flows induced by the observed centered rainfalls

Full size image
Fig. 11
figure 11

A Distribution of daily discharge (Q24) values based on SCHADEX prediction, as compared with the observed daily discharge associated with centered rainfall events (QJc), B Distribution of daily discharge values based on SCHADEX prediction in seasons (a) to (d)

Full size image
Fig. 12
figure 12

A Hydrographs selected for computing the peak-to-volume ratio, and B The scatter plot for peak-to-volume ratio

Full size image
Fig. 13
figure 13

CDF of predicted peak discharges estimated T-year floods

Full size image

Daily discharges with different return periods were estimated by different methods. These discharges were compared with the recorded discharges in hydrometric stations and also with each other to evaluate the performance of methods and select the optimal method for predicting extreme flows. A comparison of the predicted discharges 1000 years (QTr = 1000) given by the SCHADEX, GRADEX (Gradient of the Exponential Distribution), and AGREGEE methods with statistical flood frequency analysis was given in Fig. 14. A generalization of the Gradex model that is designed to estimate the flood frequency curve, for a specific duration using a combination of observed flow, rainfall, and historical information.

Fig. 14
figure 14

Comparison of the predicted Q1000 discharges given by the SCHADEX, GRADEX, AGREGEE methods with statistical flood frequency analysis (GEV, GUMBEL) based on the annual maximum series

Full size image

Discussion

The agreement between the observed and predicted distributions of peak and daily discharges is highly satisfactory. It is important to highlight that these impressive results have been achieved without any need for parameter adjustments to enhance the fit of the peak or daily distributions with the observational data. The originators of this method attribute this success to two factors: the effective use of MEWP's probabilistic rainfall model with appropriate seasonal divisions, and the optimization process of the rainfall-runoff model. The findings indicated a strong correlation between the long-term patterns of peak and daily discharge, regardless of whether the data was obtained from centered rainfall events or annual maximum sampling. The MEWP model's distributions revealed that the exponential function accurately describes the asymptotic behavior of daily discharges. Paquet et al (2013), Brigode et al. (2014), and Valent et al. (2017) also present, MEWP's probabilistic rainfall model provided satisfying results in the rainfall-runoff modeling.

The prediction of snow cover area, snow equivalent water, and runoff in the Bakhtiary watershed demonstrates improved performance during both the calibration and validation phases when utilizing semi-distributed approaches. In this updated iteration of MORDOR-SD, the equations employed have undergone revision to more accurately depict the crucial elements of hydrology, including snow and evapotranspiration. Additionally, efforts were made to minimize the number of model parameters. Furthermore, semi-distributed schemes were assessed to spatialize elevation zones. In the initial assessment, the main emphasis was on forecasting runoff using a split-sample test that considered multiple criteria. In the subsequent evaluation, two separate hydrological variables were assessed, which were not included in the model training process. Snow and evapotranspiration show some evidence for this performance in predicting the accuracy of hydrological parameters. Considering snow, evaporation, and transpiration are pieces of evidence for this performance in predicting the accuracy of hydrological parameters, which are from the results of Garavaglia et al. (2017) in 50 watersheds in France, whose average area is 911 km2 and their average height is 981 m a.s.l.

To assess the accuracy of the SCHADEX prediction, we visually assessed its performance by comparing the theoretical CDFs of the average daily flows with the observed flow or discharges linked to the central rainfall events. The results showed that when including additional information, all the modeling methods produce higher estimates compared to statistical flood frequency analysis. In particular, SCHADEX, AGREGEE, and GRADEX show significantly over estimations values. In contrast, none of the traditional methods (GEV, Gumbel), however, could successfully predict historical floods (three events on 12 Mar 2005, 30 Mar1997, and 9 Feb 2006) in Fig. 14, while interestingly GRADEX and SCHADEX completely fitted on extreme values for mentioned events.

The periods utilized for the SCHADEX predictions, which span from around 1976–2012, are slightly shorter compared to the periods employed for statistical flood frequency analysis and other modeling techniques, which cover the years 1955–2013. This discrepancy may potentially affect the assessment and comparison process. Previous research has demonstrated that when examining the sensitivity analysis of different elements within the SCHADEX method to variations in hydro-climatological conditions, it is crucial to utilize a minimum of 20–30 years of high-quality climatological data in the development of the precipitation probabilistic model (Brigode 2103; Brigode et al. 2014). Concerning the discussion by Lawrence et al. (2014) nonstationary precipitation data for SCHADEX application especially under semi-arid to arid conditions (i.e., most areas of Iran’s climate conditions) due to the most relevant result, implies that a degree of stationarity over the entire period of interest, as well as a suitable number of rainfall events for the modeling and analysis.

The SCHADEX approach can to identify potential flood risks during different seasons, which may not be accurately depicted by the annual maximum flow series. Additionally, unlike continuous prediction methods, this approach avoids the need to use a complex climatic generator to assess a series that spans an extremely long period, such as 1000 years or more, to evaluate a collection of events with high return periods.

The extreme flow rates were predicted and compared using different methods and the results showed that the methods GRADEX, AGREGEE, and SCHADEX have the highest performance in extreme flow modeling, respectively. However, rainfall-runoff models consider the advantages of their purity, such as ease of learning and use, and the possibility of evaluating different scenarios (Kayan et al. 2021; Gholami and Sahour 2021).

Conclusions

This study is the first application of the SCHADEX methodology that applied in Irena’s climate condition, if calibration and validation of the SCHADEX method in several watersheds of various climate genesis and physiography have been acceptable results, it can replace instead of FFA methods used in Iran. In parallel with the scientific evaluation of semi-continuous rainfall–runoff, prediction is actively continuing particularly, comparisons with other current methods (regional frequency analysis, or rainfall–runoff models). One disadvantage of the SCHADEX model, compared to the other prediction methods discussed, is its higher level of complexity. As a result, it may require more effort from the user, while in GRADEX and AGREGEE some parameters (i.e., precipitation and historical flood data) help to find relevant results simply. New research for verifying some assumptions for these parsimonious methods, in Iran’s climate conditions and weather genesis will be interesting in future studies. The current version of SCHADEX necessitates the utilization of recorded discharge daily for model calibration. Additionally, it requires hourly discharge data to evaluate the peak-to-volume ratio, which is essential in predicting instantaneous discharge values. However, obtaining such data is often challenging in watersheds where conceptual flood estimates are needed. The predictions of extreme values from various hydrological models in the SCHADEX study are consistent when the appropriate optimization method is used, particularly in optimizing the maximum values, and when a thorough validation of the optimization results is conducted. It is suggested for future studies the implementation of a comprehensive fully distributed model of the rainfall-runoff system, incorporating a fine time step (e.g., hourly) to encompass large-scale and ungauged watersheds. In addition, other models are used for predicting rainfall-runoff, namely IHACRES, and GR4J, which utilize rainfall, stream flow, and evaporation data to determine unit hydrographs and component flows.