Skip to main content
SpringerLink
Log in

Multiscale hydrodynamics in thrust bearing involving surface roughness

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

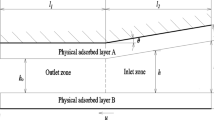
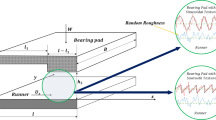
When the surface roughness is comparable to the surface separation in a hydrodynamic thrust bearing, the effect of the surface roughness should be considered. In the condition of low bearing clearances such as on the scales of 1 nm and 10 nm, normally not only the surface roughness but also the physically adsorbed layer on the bearing surface should be simultaneously considered in evaluating the bearing performance. The present paper presents the numerical calculation results of the surface roughness influences on the hydrodynamic pressure and carried load of the inclined fixed pad thrust bearing with low bearing clearances when the effect of the adsorbed layer is incorporated. It is shown that the influence of the surface roughness is strongly dependent on the adsorbed layer and it is significantly increased with the increase in the interaction strength between the fluid and the bearing surface when the bearing clearance is low. For a weak fluid-bearing surface interaction, the results are close to those obtained from the classical hydrodynamic theory indicating the increase in the hydrodynamic pressure and carried load of the bearing with the increase in the surface roughness, while for the medium or strong fluid-bearing surface interactions, this surface roughness effect is much stronger. The results reveal the new mechanism in the studied model of the bearing regarding the coupled effects of the surface roughness and the physically adsorbed layer on the bearing surface.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Abbreviations

\(a_{0},a_{1},a_{2} \) :

Constant for formulating \(C_{y} \), Eq. (10)

\(C_{q} \) :

Ratio of the average density of the adsorbed layer to the fluid bulk density, \(\rho _{{bf},K}^{{eff}}/\rho _{K}\)

\(C_{y} \) :

Ratio of the effective viscosity of the adsorbed layer to the fluid bulk viscosity, \(\eta _{{bf},K}^{{eff}} /\eta _{K}\)

D :

Fluid molecule diameter

h :

Thickness of the intermediate continuum fluid film

\(h_{bf} \) :

Adsorbed layer thickness

\(h_{cr,{bf}}\) :

Critical thickness for characterizing the rheological properties of the adsorbed layer

\(h_{o} \) :

Continuum fluid film thicknesses on the bearing exit

\(h_{t} \) :

Surface separation

\(h_{t,o} \) :

Surface separation on the bearing exit

\(H_{bf}\) :

\(h_{{bf}} /h_{cr,{bf}}\)

\(H_{t,o}\) :

\(h_{t,o} /h_{bf}\)

i, j :

Order numbers of the fluid molecules across the adsorbed layer thickness, respectively

l :

Width of the bearing

\(m_{0}, m_{1}, m_{2}, m_{3} \) :

Constant for formulating \(C_{q} \), Eq. (9)

n :

Equivalent number of the fluid molecules across the adsorbed layer thickness

N :

Maximum order number of the discretized points

p :

Hydrodynamic pressure

P :

Dimensionless hydrodynamic pressure, \(ph_{t,o} /(u\eta _{a} )\)

\(q_{0} \) :

Ratio of the neighboring fluid molecule separations across the adsorbed layer thickness, \(\Delta _{j+i} /\Delta _{j}\)

\(q_{m} \) :

Mass flow rate per unit contact length through the bearing

\(Q_{m} \) :

Dimensionless mass flow rate per unit contact length through the bearing, \(q_{m} /(u\rho _{a} h_{t,o} )\)

\(Q_{m,\max }, \quad Q_{m,\min } \) :

Upper and lower limits of the range where the real value of \(Q_{m} \) exists, respectively

\(R_{z} \) :

Maximum height of the surface roughness

u :

Sliding speed of the bearing

w :

Load per unit contact length carried by the bearing

W :

Dimensionless load, \(w/(u\eta _{a} )\)

x :

Coordinate in the flow direction

X :

Dimensionless coordinate, x/l

\(\theta \) :

Bearing tilting angle

\(\delta _{x} \) :

Distance between the neighboring discretized points in the lubricated area, l/N

\(\rho \) :

Fluid bulk density

\(\rho _{bf}^{eff}\) :

Average density of the adsorbed layer

\(\rho _{a} \) :

Fluid bulk density at atmospheric pressure

\(\eta \) :

Fluid bulk viscosity

\(\eta _{{bf}}^{{eff}} \) :

Effective viscosity of the adsorbed layer

\(\eta _{a} \) :

Fluid bulk viscosity at atmospheric pressure

\(\lambda _{bf} \) :

Ratio of the thickness of the adsorbed layer to the thickness of the intermediate continuum fluid film, \(h_{bf} /h\)

\(\Delta _{j} \) :

Separation between the \((j+1)\textrm{th}\) and \(j{\textrm{th}}\) fluid molecules across the adsorbed layer thickness

\(\Delta x\) :

Separation between the neighboring fluid molecules in the x coordinate direction in the adsorbed layer

\(\Delta _{n-2} \) :

Separation between the neighboring fluid molecules across the adsorbed layer thickness just on the boundary between the adsorbed layer and the continuum fluid

J, K :

On the Jth and Kth discretized points in the lubricated area, respectively

References

  1. White, J.W.: Analytic solution of a finite-width rough surface hydrodynamic bearing. J. Appl. Mech. 53, 450–454 (1986)

    Article  ADS  Google Scholar 

  2. Siddangouda, A., Biradar, T.V., Naduvinamani, N.B.: Combined effects of micropolarity and surface roughness on the hydrodynamic lubrication of slider bearings. J. Braz. Soc. Mech. Sci. Eng. 36, 45–58 (2014)

    Article  Google Scholar 

  3. Sinha, P., Adamu, G.: THD analysis for slider bearing with roughness: special reference to load generation in parallel sliders. Acta Mech. 207, 11–27 (2009)

    Article  Google Scholar 

  4. Kim, M., Lee, S.M., Lee, D.W., Park, S., Kim, S.: Tribological effects of a rough surface bearing using an average flow analysis with a contact model of asperities. Int. J. Precis. Eng. Manuf. 18, 99–107 (2017)

    Article  Google Scholar 

  5. Salama, M.E.: The effect of macro-roughness on the performance of parallel thrust bearings. Proc. Inst. Mech. Engs. 163, 149–161 (1950)

    Article  Google Scholar 

  6. Tzeng, S.T., Saibel, E.: Surface roughness effect on slider bearing lubrication. Trib. Trans. 10, 334–348 (1967)

    Google Scholar 

  7. Andharia, P.I., Gupta, J.L., Deheri, G.M.: Effect of surface roughness on hydrodynamic lubrication of slider bearings. Trib. Trans. 44, 291–297 (2001)

    Article  Google Scholar 

  8. Phan-Thien, N.: On the effects of the Reynolds and Stokes surface roughnesses in a two-dimensional slider bearing. Proc. Roy. Soc. Lond. A377, 349–362 (1981)

    ADS  Google Scholar 

  9. Sun, D.C., Chen, K.K.: First effects of Stokes roughness on hydrodynamic lubrication. J. Lubri. Technol. 99, 1–9 (1977)

    Google Scholar 

  10. Elrod, H.G.: Thin-film lubrication theory for Newtonian fluids with surfaces processing striated roughness or grooving. J. Lubri. Technol. 95, 484–489 (1973)

    Article  Google Scholar 

  11. Ruan, B., Salant, R.F., Green, I.: A mixed lubrication model of liquid/gas mechanical face seals. Tribol. Trans. 40, 647–657 (1997)

    Article  Google Scholar 

  12. Karupannasamy, D.K., Hol, J., de Rooij, M.B., Meinders, T., Schipper, D.J.: Modelling mixed lubrication for deep drawing processes. Wear 294–295, 296–304 (2012)

    Article  Google Scholar 

  13. Everett, D.H., Findenegg, G.H.: Calorimetric evidence for the structure of films adsorbed at the solid/liquid interface: the heats of wetting of ‘Graphon’ by some n-alkanes. Nature 223, 52–53 (1969)

    Article  ADS  Google Scholar 

  14. Brown, C.E., Everett, D.H., Powell, A.V., Thome, P.E.: Adsorption and structuring phenomena at the solid/liquid interface. Faraday Discuss. Chem. Soc. 59, 97–108 (1975)

    Article  Google Scholar 

  15. Grosse-Rhode, M., Findenegg, G.H.: Formation of ordered monolayers of \(n\)-alkanes at the cleavage face of nickel chloride. J. Colloid Interface Sci. 64, 374–376 (1978)

    Article  ADS  Google Scholar 

  16. Findenegg, G.H.: The volumetric behavior of hydrocarbon liquids near the graphon surface. J. Colloid Interface Sci. 35, 249–253 (1971)

    Article  ADS  Google Scholar 

  17. Ho, C.M., Tai, Y.C.: Micro-electro-mechanical-systems (MEMS) and fluid flows. Ann. Rev. Fluid Mech. 30, 579–612 (1998)

    Article  ADS  Google Scholar 

  18. Judy, J.W.: Microelectromechanical systems (MEMS): fabrication, design and applications. Smart Mater. Struc. 10, 1115 (2001)

    Article  ADS  Google Scholar 

  19. Chan, D.Y.C., Horn, R.G.: The drainage of thin liquid films between solid surfaces. J. Chem. Phys. 83, 5311–5324 (1985)

    Article  ADS  Google Scholar 

  20. Liu, C., Li, Z.: On the validity of the Navier-Stokes equations for nanoscale liquid flows: The role of channel size. AIP Adv. 1, 032108 (2011)

    Article  ADS  Google Scholar 

  21. Zhang, Y.B.: New explanation for the measured very low film thicknesses in lubricated concentrated contacts. J. Balkan Trib. Assoc. 27, 439–444 (2021)

    Google Scholar 

  22. Atkas, O., Aluru, N.R.: A combined continuum/DSMC technique for multiscale analysis of microfluidic filters. J. Comput. Phys. 178, 342–372 (2002)

    Article  ADS  Google Scholar 

  23. Yen, T.H., Soong, C.Y., Tzeng, P.Y.: Hybrid molecular dynamics-continuum simulation for nano/mesoscale channel flows. Microfluid. Nanofluid. 3, 665–675 (2007)

    Article  Google Scholar 

  24. Liu, J., Chen, S., Nie, X., Robbins, M.O.: A continuum-atomistic simulation of heat transfer in micro- and nano- flows. J. Comput. Phys. 227, 279–291 (2007)

    Article  ADS  Google Scholar 

  25. Zhang, Y.B.: Modeling of flow in a very small surface separation. Appl. Math. Mod. 82, 573–586 (2020)

    Article  MathSciNet  Google Scholar 

  26. Zhang, Y.B.: Multiscale hydrodynamics in line contacts. Mech. Res. Commun. 111, 103658 (2021)

    Article  ADS  Google Scholar 

  27. Zhang, Y.B.: Multiscale mixed hydrodynamics in line contacts. Continuum Mech. Thermodyn. 34, 507–518 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  28. Huang, C., Zhang, Y.B., Pang, M.J., Jiang, X.D.: Multiscale analysis of hydrodynamic fixed pad thrust slider bearing. J. Balkan Trib. Assoc. 27, 243–255 (2020)

    Google Scholar 

  29. Zhang, Y.B.: Monte Carlo simulation results of some basic physical properties of Lennard-Jones fluids. J. Mol. Liq. 128, 96–98 (2006)

    Article  Google Scholar 

  30. Zhang, Y.B.: Modeling of molecularly thin film elastohydrodynamic lubrication. J. Balkan Trib. Assoc. 10, 394–421 (2004)

    Google Scholar 

  31. Zhang, Y.B.: Lubrication analysis for a line contact covering from boundary lubrication to hydrodynamic lubrication: part I- micro contact results. J. Comput. Theor. Nanosci. 11, 62–70 (2014)

    Article  Google Scholar 

  32. Jiang, C.T., Zhang, Y.B.: Direct matching between the flow factor approach model and molecular dynamics simulation for nanochannel flows. Sci. Rep. 12, 396 (2022)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mechanical Engineering, Changzhou University, Changzhou, Jiangsu Province, China

    Chen Huang & Yongbin Zhang

Authors
  1. Chen Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongbin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yongbin Zhang.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest with this research.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, C., Zhang, Y. Multiscale hydrodynamics in thrust bearing involving surface roughness. Continuum Mech. Thermodyn. 36, 445–458 (2024). https://doi.org/10.1007/s00161-023-01275-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-023-01275-z

Keywords

Search

Navigation