Probabilistic state synthesis based on optimal convex approximation

Abstract

When preparing a pure state with a quantum circuit, there is an unavoidable approximation error due to the compilation error in fault-tolerant implementation. A recently proposed approach called probabilistic state synthesis, where the circuit is probabilistically sampled, is able to reduce the approximation error compared to conventional deterministic synthesis. In this paper, we demonstrate that the optimal probabilistic synthesis quadratically reduces the approximation error. Moreover, we show that a deterministic synthesis algorithm can be efficiently converted into a probabilistic one that achieves this quadratic error reduction. We also numerically demonstrate how this conversion reduces the T-count and analytically prove that this conversion halves an information-theoretic lower bound on the circuit size. In order to derive these results, we prove general theorems about the optimal convex approximation of a quantum state. Furthermore, we demonstrate that this theorem can be used to analyze an entanglement measure.

Introduction

The latest quantum computer applications require various nontrivial quantum states for computation, secure communication, and the fundamental investigation of quantum mechanics. Examples include the ground state (or its approximation) of a Hamiltonian, which is used to compute the ground energy in quantum chemistry¹, a graph state (or its variants^2,3), which has a wide range of applications such as measurement-based quantum computation⁴, blind computation⁵, and secret-sharing⁶, and data-hiding states, which are utilized for quantum data hiding⁷ and the study of local indistinguishability^8,9. In addition, quantum linear system solvers^10,11, which have various applications in machine learning, require a quantum state encoding classical data.

These applications have motivated researchers to optimize a subroutine that synthesizes a target quantum state. In order to capture the complexity of the state synthesis, there are extensive studies about the size and depth of a circuit consisting of a sequence of k(≤2)-qubit unitary gates needed to generate a target state by applying the circuit to a fixed state ${\left\vert 0\right\rangle }^{\otimes N}$^{12,13,14,15,16,17,18}. While these studies focus on the exact synthesis of a target state, a certain level of error is allowed in many quantum information processing protocols and algorithms. In practice, we have no choice but to approximately synthesize a target state due to imperfections and discretization when implementing unitary gates in a synthesis circuit. The imperfection of gates can be almost removed for specific unitary gates, called elementary gates, according to the nature of the system¹⁹ or the quantum error correction²⁰. The set of elementary gates is usually a finite set of unitary gates, e.g., Clifford gates (on a constant number of qubits) + T gates, which causes an approximation error when we synthesize a target state since there are infinite quantum states. We focus on the synthesis of a target state by using a finite number of perfectly implementable elementary gates. In this case, the objective of the optimization is reducing the size or depth of a circuit consisting of elementary gates in order to synthesize a target state with a certain level of approximation error. In other words, the objective is to reduce the approximation error within a fixed circuit size or depth.

Unfortunately, a simple volume consideration implies that the size of a circuit required for the approximate synthesis of a quantum state in an N-qubit system grows exponentially with N. However, it is important to optimize the state synthesis even on a small number of qubits since such small systems are often used repeatedly in quantum cryptography^6,7 and metrology^21,22 protocols. Such optimization is also beneficial to generate an intermediate quantum state required for synthesizing a state on a large system. Recently, theoretical physicists have taken an interest in the minimum circuit size or depth for the state synthesis on large systems due to its nontrivial physical interpretations^23,24,25, even if it may not be practically implementable.

The final goal of conventional synthesis algorithms is to deterministically find one of the best circuits for the approximation (even if an algorithm¹⁵ succeeds probabilistically). Thus, the minimum approximation error obtained by such deterministic state synthesis is given by $\mathop{\min }\nolimits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}$, where ϕ is a target state, ${\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}$ is the trace distance between two states ρ and σ, and X is the label set of pure states ${\hat{\phi }}_{x}$ generated by circuits ${{{{\mathcal{C}}}}}_{x}$ within a given cost, e.g., the circuit size, depth, or number of T-gates.

While it makes sense to approximate a target pure state by utilizing an approximated state generated by a single circuit, a recently proposed approach called probabilistic state synthesis probabilistically samples a circuit for the approximation. Suppose that the probabilistic algorithm independently samples a circuit ${{{{\mathcal{C}}}}}_{x}$ (generating ${\hat{\phi }}_{x}$) in accordance with a probability distribution p(x) each time the subroutine synthesizing ϕ is called. Then, each generated state is described by a mixed state ${\sum }_{x}p(x){\hat{\phi }}_{x}$. This can be interpreted as the transition from unitary errors to stochastic errors^26,27,28, and recent studies have experimentally demonstrated that this transition reduces the approximation error²⁹.

Despite its importance, the limitation of probabilistic state synthesis, especially the minimum approximation error $\mathop{\min }\nolimits_{p}{\left\Vert \phi -{\sum }_{x}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}$, remains unknown, nor is it clear how to find the optimal probability distribution p. While a few analytical results are obtained for the case of a qubit state^30,31,32 in the context of the optimal convex approximation of a quantum state, minimax optimization to compute the minimum approximation error makes analyses quite difficult in general.

Before presenting our results, we provide intuitive examples demonstrating the capability of probabilistic synthesis in Fig. 1. As a generalization of the qubit examples, we obtain the fundamental relationship between the minimum approximation errors obtained by the deterministic synthesis and the probabilistic one in the following theorem.

Fig. 1: Quadratic reduction of the approximation error by using probabilistic synthesis.

We assume that we can exactly generate an eigenstate ${\hat{\phi }}_{x}$ of the Pauli operators, represented by the six extreme points of the octahedron. We represent the Bloch sphere by a sphere with radius $\frac{1}{2}$, where the trace distance between two quantum states equals the Euclidean distance between the corresponding points. (a) We can compute $\mathop{\min }\nolimits_{p}{\left\Vert \phi -{\sum }_{x}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}={\epsilon }^{2}=\frac{1}{2\sqrt{3}}\left(\sqrt{3}-1\right)$ and $\mathop{\min }\nolimits_{x}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\epsilon$, where ϕ is the furthest state from ${\{{\hat{\phi }}_{x}\}}_{x = 1}^{6}$, represented as a large red point. (b) Suppose that the target state is chosen from ${S}_{G}:= \{\phi :\left\vert \phi \right\rangle =\cos t\left\vert 0\right\rangle +\sin t\left\vert 1\right\rangle ,t\in {\mathbb{R}}\}$, represented by a meridian. We can compute $\mathop{\min }\nolimits_{p}{\left\Vert \phi -{\sum }_{x}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}={\tilde{\epsilon }}^{2}=\frac{1}{2}\left(1-\frac{1}{\sqrt{2}}\right)$ and $\mathop{\min }\nolimits_{x}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\tilde{\epsilon }$, where ϕ is the furthest state in S_G from ${\{{\hat{\phi }}_{x}\}}_{x = 1}^{6}$, represented as a large red point.

Theorem 1

(simplified version) For any subset ${\{{\hat{\phi }}_{x}\}}_{x\in X}$ of pure states, it holds that

$$\mathop{\max }\limits_{\phi }\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\max }\limits_{\phi }\mathop{\min }\limits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{\,{{\mbox{tr}}}\,}^{2},$$

(1)

where the maximization of ϕ is taken over the set of pure states.

This theorem compares the worst approximation errors occurring when one synthesizes the target state that is most difficult to approximate by using ${\{{\hat{\phi }}_{x}\}}_{x}$. It implies that the optimal probabilistic synthesis always quadratically reduces the worst approximation error, moreover, it is impossible to further reduce the approximation error.

In many cases, there is no need to synthesize all possible pure states. Instead, it is more useful to understand the limitations of probabilistic synthesis when a target state is chosen from a subset S_G of pure states. As shown in Fig. 1b, we can also anticipate the quadratic error reduction in this scenario. This expectation is confirmed in the comprehensive version of Theorem 1, which includes the case of Fig. 1b.

The technique used to prove Theorem 1 is also applicable to analyzing the minimum trace distance between a general mixed state ρ and a convex hull of ${\{{\hat{\phi }}_{x}\}}_{x}$. For example, we can analyze the entanglement measure by setting ${\{{\hat{\phi }}_{x}\}}_{x\in X}$ to be the set of pure product states. As a byproduct, we obtain

$$\begin{array}{r}\mathop{\min }\limits_{\sigma \in {{{\bf{SEP}}}}}{\left\Vert {\rho }_{q}^{{{{\rm{WER}}}}}-\sigma \right\Vert }_{{{\mbox{tr}}}}=q-\frac{1}{2},\,\,\mathop{\min }\limits_{\sigma \in {{{\bf{SEP}}}}}{\left\Vert {\rho }_{q}^{{{{\rm{ISO}}}}}-\sigma \right\Vert }_{{{\mbox{tr}}}}=\frac{{d}^{2}-1}{{d}^{2}}\left(q-\frac{1}{d+1}\right),\end{array}$$

(2)

where SEP represents the set of separable states, ${\rho }_{q}^{{{{\rm{WER}}}}}$ and ${\rho }_{q}^{{{{\rm{ISO}}}}}$ represent the Werner and isotropic state with a parameter q, respectively. These coincide with a conjecture numerically found in³³. Moreover, we provide alternate succinct proof about a recently identified coincidence between the entanglement measure and coherence measure³⁴.

We also show an efficient way to convert a deterministic state synthesis algorithm into a probabilistic one that achieves quadratic error reduction. We assume there exists a deterministic state synthesis algorithm ${{{\mathcal{D}}}}$ with

INPUT: a target pure state ϕ in a constant number of qubits and target approximation error ϵ,

OUTPUT: circuit ${{{{\mathcal{C}}}}}_{x}$ (generating ${\hat{\phi }}_{x}$)

such that ${\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$ and a matrix representation of ${\hat{\phi }}_{x}$ can be obtained within runtime $polylog\left(\frac{1}{\epsilon }\right)$. We can construct ${{{\mathcal{D}}}}$ by combining algorithms to generate an exact synthesis circuit where arbitrary unitary transformations on a constant number of qubits are allowed^{12,13,14,15,16,17,18} with the Solovay-Kitaev algorithm³⁵ to decompose the unitary transformations into a sequence of elementary gates. Recent numerical analysis suggests that we could construct better ${{{\mathcal{D}}}}$ that reduces the size of a synthesis circuit by skipping the exact synthesis as an intermediate step^17,36. The efficient conversion is shown in the following theorem.

Theorem 2

(informal version) There exists a probabilistic state synthesis algorithm ${{{\mathcal{P}}}}$ that calls a deterministic state synthesis algorithm ${{{\mathcal{D}}}}$ as an oracle, and has

INPUT: a target pure state ϕ in a constant number of qubits and target approximation error ϵ

OUTPUT: circuit ${{{{\mathcal{C}}}}}_{x}$ (generating ${\hat{\phi }}_{x}$) sampled in accordance with probability distribution $\hat{p}:\hat{X}\to [0,1]$

such that ${{{\mathcal{P}}}}$ satisfies the following properties:

• Efficiency: ${{{\mathcal{P}}}}$ calls ${{{\mathcal{D}}}}$ constant times, and runtime of ${{{\mathcal{P}}}}$ is $polylog\left(\frac{1}{\epsilon }\right)$,

• Quadratic improvement: The approximation error ${\left\Vert \phi -{\sum }_{x\in \hat{X}}\hat{p}(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}$ obtained with this algorithm is upper bounded by ϵ², whereas $\mathop{\min }\nolimits_{x\in \hat{X}}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$.

Since probabilistic state synthesis reduces the approximation error, it also reduces the size of a circuit to approximately generate a target state for a given approximation error. However, the reduction rate depends on the circuit’s construction, e.g., what kind of elementary gates and synthesis algorithms are used. Since there is an established way to synthesize a single qubit state by using Clifford + T gates, we perform a numerical simulation to demonstrate how the probabilistic synthesis reduces the number of T-gates, called a T-count, for a randomly selected target state in S_G defined in Fig. 1b.

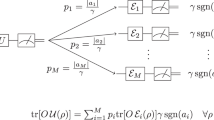
As a rigorous estimation, we also analyze a universal lower bound on the size of synthesis circuits obtained by regarding the circuit as a classical encoding of a pure state, where a description of a circuit ${{{{\mathcal{C}}}}}_{x}$ and the state ${\hat{\phi }}_{x}$ generated by ${{{{\mathcal{C}}}}}_{x}$ correspond to a label encoding a pure state and the reconstructed state by a decoder, respectively. To analyze how probabilistic synthesis reduces this lower bound, we investigate the minimum length of classical bit strings that encodes a pure state ϕ so as to approximately reconstruct the original state as shown in Fig. 2.

Fig. 2: Probabilistic encoding of pure state ϕ on a d-dimensional system using n-bit strings and a decoder Γ that generates an approximated state $\hat{\rho }$.

State ϕ is probabilistically encoded in label x in a finite set X in accordance with probability distribution p_ϕ: X → [0, 1]. As a special case of probabilistic encoding, we also consider deterministic encoding that utilizes probability distribution p_ϕ: X → {0, 1}. Note that the length of classical bit strings to represent x ∈ X is given by $n=\lceil {\log }_{2}| X| \rceil$.

We compare two types of encoding: (1) deterministic encoding that associates each ϕ to a single label x, and (2) probabilistic encoding that associates each ϕ to a label x in accordance with a probability distribution p_ϕ(x). The decoder Γ generates, in general, a mixed state ${\hat{\rho }}_{x}$ based on the input label x. Thus, the reconstructed state in the deterministic and probabilistic encoding is given by $\hat{\rho }={\hat{\rho }}_{x}$ and $\hat{\rho }={\sum }_{x}{p}_{\phi }(x){\hat{\rho }}_{x}$, respectively. In the following theorem, we show that probabilistic encoding exactly halves the bit length required for deterministic encoding in the asymptotic limits.

Theorem 3

(simplified version) Let ${n}_{\det }$ (or n_prob) be the minimum bit length required for deterministic (or probabilistic) encoding that reconstructs a state $\hat{\rho }$ satisfying ${\left\Vert \phi -\hat{\rho }\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$ for any pure state ϕ in a d-dimensional Hilbert space. Then, it holds that

$$\mathop{\lim }\limits_{\epsilon \to 0}\frac{{n}_{{{{\rm{prob}}}}}}{{n}_{\det }}=\mathop{\lim }\limits_{d\to \infty }\frac{{n}_{{{{\rm{prob}}}}}}{{n}_{\det }}=\frac{1}{2}.$$

(3)

Although several probabilistic synthesis methods suggest that the approximation error can be reduced from ϵ into O(ϵ²)^{26,27,28,29,37,38}, these methods are not applicable for analyzing the achievable minimum approximation error. This is mainly because the prior research relies on the first-order approximation to show the error reduction, which provides little information about the lower bound on the error reduction. The achievable minimum approximation error for the probabilistic unitary synthesis has been obtained by us³⁹. However, this result cannot be directly applied to the state synthesis since the generated state in state synthesis is obtained by applying a gate sequence to a fixed input state while the approximation error in unitary synthesis is quantified for the worst input state. Moreover, a target state could be approximated by probabilistically mixing two unitary transformations whose behaviors are totally different, except for the fixed input state.

In the proof of Theorem 1, we analyze the minimum approximation error $\mathop{\min }\nolimits_{p}{\left\Vert \phi -{\sum }_{x}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\min }\nolimits_{p}\mathop{\max }\nolimits_{0\le M\le {\mathbb{I}}}tr\left[M(\phi -{\sum }_{x}p(x){\hat{\phi }}_{x})\right]$, which contains minimax optimization by definition. The main tool for the analysis is the strong duality of semidefinite programming. This enables us to formulate the minimum approximation error as a semidefinite program (SDP). Moreover, we show that the SDP can be dramatically simplified when both ϕ and ${\{{\hat{\phi }}_{x}\}}_{x}$ exhibit symmetry. As discussed in the previous subsection, these techniques can be utilized to analyze the minimum trace distance between a general mixed state and a convex set, such as the set of separable states.

The reformulation of the minimum approximation error as an SDP enables us to compute the optimal probability distribution to achieve it efficiently. By using Theorem 1, we can verify that by solving this SDP with ${\{{\hat{\phi }}_{x}\}}_{x\in X}$ satisfying $\mathop{\max }\nolimits_{\phi }\mathop{\min }\nolimits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$, which is called an ϵ-covering, we obtain a probability distribution $\hat{p}$ that achieves quadratic reduction of the approximation error, i.e., ${\left\Vert \phi -{\sum }_{x\in X}\hat{p}(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le {\epsilon }^{2}$. However, the size of this SDP is too large to achieve the efficiency shown in Theorem 2, since the size ∣X∣ of the ϵ-covering is ${\left(\frac{1}{\epsilon }\right)}^{\Omega (1)}$. This problem can be resolved by proving that any ${\hat{\phi }}_{x}$ in the support of the optimal probability distribution in the minimum approximation error is close to ϕ; more precisely, ${\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le 2\epsilon$. This enables us to construct a modified SDP whose size is independent of ϵ.

Theorem 3 is obtained by combining Theorem 1 with the estimation of the minimum size of the ϵ-covering. Due to its prominent role in algorithm design and asymptotic geometric analysis, the order of the minimum size of the ϵ-covering has been well-studied^40,41,42. However, to obtain Theorem 3, we precisely analyze the constant factor in the order, which refines the previous estimations^40,41.

Results

Preliminaries

We consider only finite-dimensional Hilbert spaces in this paper. The two-dimensional Hilbert space ${{\mathbb{C}}}^{2}$ is called a qubit. ${{{\bf{L}}}}\left({{{\mathcal{H}}}}\right)$ and ${{{\bf{Pos}}}}\left({{{\mathcal{H}}}}\right)$ represent the set of linear operators and positive semidefinite operators on Hilbert space ${{{\mathcal{H}}}}$, respectively. ${\mathbb{I}}\in {{{\bf{Pos}}}}\left({{{\mathcal{H}}}}\right)$ represents the identity operator. For Hermitian operators A and B on ${{{\mathcal{H}}}}$, A ≥ B represents $A-B\in {{{\bf{Pos}}}}\left({{{\mathcal{H}}}}\right)$, and A > B means A − B is positive definite. ${{{\bf{S}}}}\left({{{\mathcal{H}}}}\right):= \left\{\rho \in {{{\bf{Pos}}}}\left({{{\mathcal{H}}}}\right):tr\left[\rho \right]=1\right\}$ and ${{{\bf{P}}}}\left({{{\mathcal{H}}}}\right):= \left\{\rho \in {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right):tr\left[{\rho }^{2}\right]=1\right\}$ represent the set of quantum states and pure states, respectively. Pure state $\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)$ is sometimes alternatively represented by complex unit vector $\left\vert \phi \right\rangle \in {{{\mathcal{H}}}}$ satisfying $\phi =\left\vert \phi \right\rangle \left\langle \phi \right\vert$.

The trace distance ${\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}$ of two quantum states $\rho ,\sigma \in {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)$ is defined as ${\left\Vert M\right\Vert }_{{{\mbox{tr}}}}:= \frac{1}{2}tr\left[\sqrt{M{M}^{{\dagger} }}\right]$ for $M\in {{{\bf{L}}}}\left({{{\mathcal{H}}}}\right)$. It represents the maximum total variation distance between probability distributions obtained by measurements performed on two quantum states. Thus, it satisfies ${\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}=\mathop{\max }\nolimits_{0\le M\le {\mathbb{I}}}tr\left[M(\rho -\sigma )\right]$. A similar notion measuring the distinguishability of ρ and σ is the fidelity function, defined by $F\left(\rho ,\sigma \right):= \max tr\left[{\Phi }^{\rho }{\Phi }^{\sigma }\right]$, where ${\Phi }^{\rho }\in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\otimes {{{{\mathcal{H}}}}}^{{\prime} }\right)$ is a purification of ρ, i.e., $\rho ={{{\mbox{tr}}}}_{{{{{\mathcal{H}}}}}^{{\prime} }}\left[{\Phi }^{\rho }\right]$, and the maximization is taken over all the purifications. Fuchs-van de Graaf inequalities⁴³ provide relationships between the two measures with respect to the distinguishability as follows:

$$1-\sqrt{F\left(\rho ,\sigma \right)}\le {\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}\le \sqrt{1-F\left(\rho ,\sigma \right)}$$

(4)

holds for any states $\rho ,\sigma \in {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)$, where the equality of the right inequality holds when ρ and σ are pure.

An operator $A:{{{\mathcal{H}}}}\to {{{\mathcal{H}}}}$ is called antilinear if it satisfies $A(\alpha \left\vert \phi \right\rangle +\beta \left\vert \psi \right\rangle )={\alpha }^{* }A\left\vert \phi \right\rangle +{\beta }^{* }A\left\vert \psi \right\rangle$, where α^* represents the complex conjugate of $\alpha \in {\mathbb{C}}$. The Hermitian adjoint A^† of an antilinear operator A is defined by $\left\langle \psi \right\vert {A}^{{\dagger} }\left\vert \phi \right\rangle =\left\langle \phi \right\vert A\left\vert \psi \right\rangle$. An antilinear operator U is called antiunitary if it satisfies ${U}^{{\dagger} }U={\mathbb{I}}$. An antiunitary operator Θ is called a conjugation if it satisfies Θ^† = Θ. An example of a conjugation is the complex conjugation θ with respect to the computational basis. Note that for Hermitian operators M₁ and M₂ and an antilinear operator A, the cyclic property $tr\left[{M}_{1}A{M}_{2}{A}^{{\dagger} }\right]=tr\left[{A}^{{\dagger} }{M}_{1}A{M}_{2}\right]$ of the trace holds.

Quadratic reduction of approximation error

We first show the lower bound of the approximation error obtained by the optimal probabilistic mixture in the following lemma.

Lemma 1

For a finite set ${\{{\hat{\phi }}_{x}\}}_{x\in X}\subseteq {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)$ of pure states and a pure state $\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)$, it holds that

$$\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\ge \mathop{\min }\limits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{\,{{\mbox{tr}}}\,}^{2}.$$

(5)

Proof

Let p minimize the left-hand side of Eq. (5). The following calculation completes the proof.

$$(L.H.S.)\ge \left(1-\mathop{\sum}\limits_{x\in X}p(x)tr\left[\phi {\hat{\phi }}_{x}\right]\right)\ge \mathop{\min }\limits_{x\in X}\left(1-F\left(\phi ,{\hat{\phi }}_{x}\right)\right)=(R.H.S.),$$

(6)

where we use ${\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}\ge \mathop{\max }\nolimits_{\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)}tr\left[\phi (\rho -\sigma )\right]$ in the first inequality and use the right equality in Ineq. (4) in the last equality. □

This lemma shows that the reduction rate of the approximation error by using probabilistic synthesis is, at best, quadratic. However, the two examples given in Fig. 1 indicate that a precisely quadratic reduction is possible if we consider the worst approximation error occurring when we synthesize the target state that is most difficult to approximate in a particular subset S_G of states. To achieve the quadratic reduction, it is important to carefully select S_G. We use group symmetries in the following lemma to characterize S_G and prove the quadratic reduction. This characterization also makes it easier to apply this lemma to various settings in the state synthesis.

Lemma 2

Let X be a finite set, G be a finite subgroup of unitary and antiunitary operators, and ${S}_{G}:= \{\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right):\forall U\in G,[U,\phi ]=0\}$ be the set of pure states invariant under the action of G. If a set ${\{{\hat{\phi }}_{x}\in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)\}}_{x\in X}$ of pure states is invariant under the action of G, i.e., ${\{{\hat{\phi }}_{x}\}}_{x\in X}={\{U{\hat{\phi }}_{x}{U}^{{\dagger} }\}}_{x\in X}$ for all U ∈ G, it holds that

$$\mathop{\max }\limits_{\phi \in {S}_{G}}\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\max }\limits_{\phi \in {S}_{G}}\mathop{\min }\limits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{\,{{\mbox{tr}}}\,}^{2}.$$

(7)

Lemma 2 is a direct consequence of the following lemma for computing the minimum trace distance between a mixed state and a convex subset of mixed states.

Lemma 3

Let X be a finite set and G be a finite subgroup of unitary and antiunitary operators. Let P_G be the set of positive semidefinite operators invariant under the action of G, i.e., ${P}_{G}:= \{P\in {{{\bf{Pos}}}}\left({{{\mathcal{H}}}}\right):\forall U\in G,[U,P]=0\}$. If $\rho \in {P}_{G}\cap {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)$ and a set ${\{{\hat{\rho }}_{x}\in {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)\}}_{x\in X}$ of mixed states is invariant under the action of G, i.e., ${\{{\hat{\rho }}_{x}\}}_{x\in X}={\{U{\hat{\rho }}_{x}{U}^{{\dagger} }\}}_{x\in X}$ for all U ∈ G, it holds that

$$\mathop{\min }\limits_{p}{\left\Vert \rho -\mathop{\sum}\limits_{x\in X}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\max }\limits_{0\le M\le {\mathbb{I}}\atop M\in {P}_{G}}\left(tr\left[M\rho \right]-\mathop{\max }\limits_{x\in X}tr\left[M{\hat{\rho }}_{x}\right]\right),$$

(8)

where the minimization is taken over a probability distribution p over X. In particular, when ρ is a pure state ϕ, it holds that

$$\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\max }\limits_{\psi \in {P}_{G}\cap {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)}\left(tr\left[\psi \phi \right]-\mathop{\max }\limits_{x\in X}tr\left[\psi {\hat{\rho }}_{x}\right]\right).$$

(9)

Proof

We start from a mixed state ρ. By using the minimax theorem, we obtain

$$(L.H.S.\,of\,Eq.(8))=\mathop{\min }\limits_{p}\mathop{\max }\limits_{0\le M\le {\mathbb{I}}}\left(tr\left[M\rho \right]-\mathop{\sum}\limits_{x\in X}p(x)tr\left[M{\hat{\rho }}_{x}\right]\right)$$

(10)

$$=\mathop{\max }\limits_{0\le M\le {\mathbb{I}}}\mathop{\min }\limits_{p}\left(tr\left[M\rho \right]-\mathop{\sum}\limits_{x\in X}p(x)tr\left[M{\hat{\rho }}_{x}\right]\right)$$

(11)

$$=\mathop{\max }\limits_{0\le M\le {\mathbb{I}}}\left(tr\left[M\rho \right]-\mathop{\max }\limits_{x\in X}tr\left[M{\hat{\rho }}_{x}\right]\right).$$

(12)

This proves (L. H. S. ) ≥ (R. H. S. ). Let M maximize Eq. (12). Due to the invariance of ρ and ${\{{\hat{\rho }}_{x}\}}_{x}$ under the action of G, we can verify that U^†MU also maximizes Eq. (12). By defining $\hat{M}=\frac{1}{| G| }{\sum }_{U\in G}{U}^{{\dagger} }MU$, we obtain

$$\begin{array}{l}(R.H.S.\,of\,Eq.(8))\,\ge \,tr\left[\hat{M}\rho \right]-\mathop{\max }\limits_{x\in X}tr\left[\hat{M}{\hat{\rho }}_{x}\right]=tr\left[M\rho \right]-\mathop{\max }\limits_{x\in X}\left(\frac{1}{| G| }\mathop{\sum}\limits_{U\in G}tr\left[MU{\hat{\rho }}_{x}{U}^{{\dagger} }\right]\right)\\ \qquad\qquad\qquad\qquad\quad \,\ge \, tr\left[M\rho \right]-\frac{1}{| G| }\mathop{\sum}\limits_{U\in G}\mathop{\max }\limits_{x\in X}tr\left[MU{\hat{\rho }}_{x}{U}^{{\dagger} }\right]\\ \qquad\qquad\qquad\qquad\quad\,=\,tr\left[M\rho \right]-\mathop{\max }\limits_{x\in X}tr\left[M{\hat{\rho }}_{x}\right]=(L.H.S.\,of\,Eq.(8)),\end{array}$$

(13)

where we use Eq. (12) in the last equality.

When ρ is a pure state ϕ, we can derive

$$(L.H.S.\,of\,Eq.(9))=\mathop{\max }\limits_{\sigma \in {P}_{G}\cap {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)}\left(tr\left[\sigma \phi \right]-\mathop{\max }\limits_{x\in X}tr\left[\sigma {\hat{\rho }}_{x}\right]\right)$$

(14)

by the same argument starting from

$$(L.H.S.\,of\,Eq.(9))=\mathop{\min }\limits_{p}\mathop{\max }\limits_{\sigma \in {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)}tr\left[\sigma \left(\phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\rho }}_{x}\right)\right]=\mathop{\max }\limits_{\sigma \in {{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)}\left(tr\left[\sigma \phi \right]-\mathop{\max }\limits_{x\in X}tr\left[\sigma {\hat{\rho }}_{x}\right]\right),$$

(15)

where we use the fact that the dimension of the eigenspace of $\phi -{\sum }_{x\in X}p(x){\hat{\rho }}_{x}$ associated with positive eigenvalues is zero or one in the first equality, and use the minimax theorem in the second equality. We complete the proof of Eq. (9) by using the following observation: When (L. H. S. of Eq. (9)) = 0, Eq. (9) holds since there exists x ∈ X such that ${\hat{\rho }}_{x}=\phi$. When (L. H. S. of Eq. (9)) > 0, σ maximizing Eq. (14) is a pure state. For if σ with ${\left\Vert \sigma \right\Vert }_{\infty } < 1$ maximizes Eq. (14), we can show a contradiction by setting ρ = ϕ and $M=\frac{\sigma }{{\left\Vert \sigma \right\Vert }_{\infty }}$ in Eq. (12). □

Proof of Lemma 2

By setting ${\hat{\rho }}_{x}$ in Eq. (9) to be ${\hat{\phi }}_{x}$, we obtain

$$\begin{array}{rcl}\mathop{\max }\limits_{\phi \in {S}_{G}}\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}&=&\mathop{\max }\limits_{\psi \in {S}_{G}}\left(\mathop{\max }\limits_{\phi \in {S}_{G}}tr\left[\psi \phi \right]-\mathop{\max }\limits_{x\in X}tr\left[\psi {\hat{\phi }}_{x}\right]\right)\\ &=&1-\mathop{\min }\limits_{\psi \in {S}_{G}}\mathop{\max }\limits_{x\in X}tr\left[\psi {\hat{\phi }}_{x}\right]=\mathop{\max }\limits_{\psi \in {S}_{G}}\mathop{\min }\limits_{x\in X}{\left\Vert \psi -{\hat{\phi }}_{x}\right\Vert }_{\,{{\mbox{tr}}}\,}^{2},\end{array}$$

(16)

where we use the right equality in Ineq. (4) in the last equality. □

As consequences of Lemma 2 or Lemma 3, we obtain the following implications.

• 1. When $G=\{{\mathbb{I}}\}$, we obtain ${S}_{G}={{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)$. This case is applicable to any ${\{{\hat{\phi }}_{x}\}}_{x\in X}$ and proves the quadratic reduction of the approximation error given in Fig. 1(a).

• 2. When $G=\{{\mathbb{I}},\theta \}$ with the complex conjugation θ, we obtain ${S}_{G}=\{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{2}\right):\left\vert \phi \right\rangle =\cos t\left\vert 0\right\rangle +\sin t\left\vert 1\right\rangle ,t\in {\mathbb{R}}\}$. In this case, the quadratic reduction of the worst approximation error occurring when we synthesize a target state in S_G is possible if ${\{{\hat{\phi }}_{x}\}}_{x}$ is reflection-symmetric with respect to the XZ-plane in the Bloch representation. This proves the quadratic reduction of the approximation error given in Fig. 1b. In general, conjugation-invariant pure states are often utilized in the optimal parameter estimation²².

• 3. When $G=\{{\mathbb{I}},2\Pi -{\mathbb{I}}\}$ with Hermitian projector Π whose range is ${{{\mathcal{V}}}}$, ${S}_{G}=\{\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right):\left\vert \phi \right\rangle \in {{{\mathcal{V}}}}\vee \left\vert \phi \right\rangle \in {{{{\mathcal{V}}}}}_{\perp }\}$. In this case, the quadratic reduction of the worst approximation error occurring when we synthesize a target state in ${{{\mathcal{V}}}}$ is possible if ${\{{\hat{\phi }}_{x}\}}_{x}$ is reflection-symmetric under the action of $2\Pi -{\mathbb{I}}$. This is because

  $$\mathop{\max }\limits_{\left\vert \phi \right\rangle \in {{{\mathcal{V}}}}}\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\max }\limits_{\psi \in {S}_{G}}\left(\mathop{\max }\limits_{\left\vert \phi \right\rangle \in {{{\mathcal{V}}}}}tr\left[\psi \phi \right]-\mathop{\max }\limits_{x\in X}tr\left[\psi {\hat{\phi }}_{x}\right]\right)$$

  (17)
  $$=\mathop{\max }\limits_{\left\vert \psi \right\rangle \in {{{\mathcal{V}}}}}\left(\mathop{\max }\limits_{\left\vert \phi \right\rangle \in {{{\mathcal{V}}}}}tr\left[\psi \phi \right]-\mathop{\max }\limits_{x\in X}tr\left[\psi {\hat{\phi }}_{x}\right]\right)$$

  (18)
  $$=1-\mathop{\min }\limits_{\left\vert \psi \right\rangle \in {{{\mathcal{V}}}}}\mathop{\max }\limits_{x\in X}tr\left[\psi {\hat{\phi }}_{x}\right]=\mathop{\max }\limits_{\left\vert \phi \right\rangle \in {{{\mathcal{V}}}}}\mathop{\min }\limits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{\,{{\mbox{tr}}}\,}^{2},$$

  (19)

  where we use Eq. (9) in the first equation. In general, preparing a state in a particular subspace is a widely used subroutine in various quantum information processing tasks.

We obtain the following theorem as a summary of Lemmas 1 and 2.

Theorem 1

Let X be a finite set, G be a finite subgroup of unitary and antiunitary operators, and ${S}_{G}:= \{\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right):\forall U\in G,[U,\phi ]=0\}$ be the set of pure states invariant under the action of G. If ϕ ∈ S_G and ${\{{\hat{\phi }}_{x}\in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)\}}_{x\in X}={\{U{\hat{\phi }}_{x}{U}^{{\dagger} }\}}_{x\in X}$ for all U ∈ G, it holds that

$${\epsilon }_{\phi }^{2}\le \mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le {\epsilon }_{G}^{2}\,\,\,{{{\rm{with}}}}\,{\epsilon }_{\phi }=\mathop{\min }\limits_{x\in X}{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}},\,{\epsilon }_{G}=\mathop{\max }\limits_{\psi \in {S}_{G}}\mathop{\min }\limits_{x\in X}{\left\Vert \psi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}.$$

(20)

This theorem indicates that by using mixed states, we can reduce the approximation error with respect to the trace distance. When attempting to estimate the expectation value $tr\left[O\phi \right]$ of an observable O for ϕ, this theorem implies that the bias of the expectation value can be reduced by using ${\sum }_{x\in X}p(x){\hat{\phi }}_{x}$ instead of using ${\hat{\phi }}_{x}$ as a substitute of ϕ.

Efficient probabilistic state synthesis algorithm

In this section, we present an efficient method for converting any deterministic state synthesis algorithm, denoted as ${{{\mathcal{D}}}}$, into a probabilistic one. If it takes $polylog\left(\frac{1}{\epsilon }\right)$-time for ${{{\mathcal{D}}}}$ to achieve an approximation error ϵ with an l(ϵ)-size circuit such as the Solovay-Kitaev algorithm, then our method allows us to construct a probabilistic synthesis algorithm that achieves an approximation error ϵ² by sampling l(ϵ)-size circuits, with a total runtime of $polylog\left(\frac{1}{\epsilon }\right)$.

Note that our method assumes the target state is taken from a constant-dimensional Hilbert space. As mentioned in the introduction, constant-qubits states are commonly utilized in quantum cryptography and metrology protocols. Although the existence of highly complex pure states results in an exponential runtime with respect to the number of qubits for any state synthesis algorithms, we discuss the potential of probabilistic state synthesis for a high dimensional system in Supplementary Note 3. Our conversion is based on the following proposition and lemma.

Proposition 1

Let ρ and ${\{{\hat{\rho }}_{x}\}}_{x\in X}$ be a target mixed state and a finite set of mixed states in ${{{\bf{S}}}}\left({{{\mathcal{H}}}}\right)$, respectively. Then, distance $\mathop{\min }\nolimits_{p}{\left\Vert \rho -{\sum }_{x\in X}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}$ and the optimal probability distribution {p(x)}_x∈X, which minimizes the distance, can be computed with the following SDP:

$$\begin{array}{ll} {\underline{ {\rm{Primal}}\,{\rm{problem}}}} & {\underline{{\rm{Dual}}\,{\rm{problem}}}}\\ {{\rm{maximize}}}: tr[{M\rho}]-t & {{\rm{minimize}}}: tr[{Y}]\\ {{\text{subject to}}}: 0\leq M\leq {\mathbb{I}},& {{\text{subject to}}}: Y\geq0\wedge Y\geq \rho-\sum_{x\in X}p(x){\hat{\rho}}_x,\\ \forall x\in X,tr[{M{\hat{\rho}}_x}]\leq t.& \forall x\in X,p(x)\geq0,\\ &\sum_{x\in X}p(x)\leq 1. \end{array}$$

(21)

Note that the strong duality holds in this SDP, i.e., the optimum primal and dual values are equal.

Proof

Recall that for two states ρ and σ, ${\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}$ can be computed by the following SDP:

$$\begin{array}{ll} {\underline{{{\rm{Primal}}\,{\rm{problem}}}}} & {\underline{{{\rm{Dual}}\,{\rm{problem}}}}}\\ {{\rm{maximize}}}: tr[{M(\rho-\sigma)}] & {{\rm{minimize}}}: tr[{Y}]\\ {{\rm{subject}}\,{\rm{to}}}: 0\leq M\leq {\mathbb{I}},& {\rm{subject}}\,{\rm{to}}: Y\geq0\wedge Y\geq \rho-\sigma. \end{array}$$

A formal SDP and proof of the strong duality are provided in Supplementary Note 1.

By extending the dual problem of this SDP to include the minimization of probability distribution {p(x)}_x∈X, we obtain Eq. (21). Note that the last condition ∑_x∈Xp(x) ≤ 1 in the dual problem is different from the condition ∑_x∈Xp(x) = 1 of a probability distribution; however, the optimum dual value can be achieved under the latter condition. Again, a formal SDP and proof of the strong duality are provided in Supplementary Note 1.□

Lemma 4

Let G be a finite subgroup of unitary and antiunitary operators, and ${S}_{G}:= \{\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right):\forall U\in G,[U,\phi ]=0\}$ be the set of pure states invariant under the action of G. For a positive number ϵ > 0, if ϕ ∈ S_G and ${\{{\hat{\phi }}_{x}\}}_{x\in X}$ is a finite ϵ-covering of S_G that is invariant under the action of G, i.e., $\mathop{\max }\nolimits_{\psi \in {S}_{G}}\mathop{\min }\nolimits_{x\in X}{\left\Vert \psi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$ and ${\{{\hat{\phi }}_{x}\}}_{x\in X}={\{U{\hat{\phi }}_{x}{U}^{{\dagger} }\}}_{x\in X}$ for all U ∈ G, then

$$\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}=\mathop{\min }\limits_{\hat{p}}{\left\Vert \phi -\mathop{\sum}\limits_{x\in \hat{X}}\hat{p}(x){\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}$$

(22)

holds, where $\hat{X}:= \{x\in X:{\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le 2\epsilon \}$ and the minimization of p and $\hat{p}$ are taken over probability distributions over X and $\hat{X}$, respectively.

To understand this lemma, it is helpful to refer to the examples shown in Fig. 1. If the goal is to optimally approximate a target state ϕ depicted by the red point in (a) (or (b)), it is sufficient to mix three (or two) Pauli eigenstates that are 2ϵ (or $2\tilde{\epsilon }$) close to ϕ. This fact is shown to be true for any target state in this lemma, and its proof can be found in Supplementary Note 2 as it involves technical details.

By combining Proposition 1 and Lemma 4, we can efficiently convert a deterministic state synthesis algorithm into a probabilistic one. We assume there exists a deterministic state synthesis algorithm ${{{\mathcal{D}}}}$ with

INPUT: a target pure state ϕ ∈ S_G in a constant-dimensional Hilbert space and a target approximation error $\epsilon \in \left(0,1\right)$

OUTPUT: a set ${\{{{{{\mathcal{C}}}}}_{x}^{(U)}\}}_{U\in G}$ of circuits (generating $U{\hat{\phi }}_{x}{U}^{{\dagger} }$)

such that ${\left\Vert \phi -{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$ and a matrix representation of $U{\hat{\phi }}_{x}{U}^{{\dagger} }$ can be obtained within runtime $polylog\left(\frac{1}{\epsilon }\right)$, where G is a finite subgroup of unitary and antiunitary operators and S_G is the set of pure states invariant under the action of G.

Theorem 2

For a given gate set, there exists a probabilistic state synthesis algorithm ${{{\mathcal{P}}}}$ that calls a deterministic synthesis algorithm ${{{\mathcal{D}}}}$ as an oracle, and has

INPUT: a target pure state ϕ ∈ S_G in a constant-dimensional Hilbert space, a target approximation error $\epsilon \in \left(0,1\right)$, and precision $\delta \in \left(0,1\right)$

OUTPUT: circuit ${{{{\mathcal{C}}}}}_{x}$ (generating ${\hat{\rho }}_{x}$) sampled from a set $\hat{X}$ in accordance with probability distribution $\hat{p}:\hat{X}\to [0,1]$

such that ${{{\mathcal{P}}}}$ satisfies the following properties:

• Efficiency: ${{{\mathcal{P}}}}$ calls ${{{\mathcal{D}}}}$ a constant number of times, and runtime of ${{{\mathcal{P}}}}$ is $poly\left(\log \left(\frac{1}{\epsilon }\right),\log \left(\frac{1}{\delta }\right)\right)$,

• Quadratic improvement: The approximation error ${\left\Vert \phi -{\sum }_{x\in \hat{X}}\hat{p}(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}$ obtained by ${{{\mathcal{P}}}}$ is upper bounded by ϵ² + δ, whereas $\mathop{\min }\nolimits_{x\in \hat{X}}{\left\Vert \phi -{\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon$.

Proof

In the following, we explicitly construct the algorithm.

• 1. Set free parameters c > 0 and ${c}^{{\prime} }\, > \,0$ satisfying $c+{c}^{{\prime} }\le 1$.

• 2. Generate a list ${\{{\phi }_{x}\}}_{x\in \tilde{X}}\subseteq {S}_{G}$ such that for any ψ ∈ S_G, $\mathop{\min }\nolimits_{x\in \tilde{X}}{\left\Vert \psi -{\phi }_{x}\right\Vert }_{{{\mbox{tr}}}}\le c\epsilon$ if ${\left\Vert \phi -\psi \right\Vert }_{{{\mbox{tr}}}}\le 2\epsilon$. That is, ${\{{\phi }_{x}\}}_{x\in \tilde{X}}$ is a (cϵ)-covering of $\{\psi \in {S}_{G}:{\left\Vert \phi -\psi \right\Vert }_{{{\mbox{tr}}}}\le 2\epsilon \}$.

• 3. Call ${{{\mathcal{D}}}}$ to find ${{{{\mathcal{C}}}}}_{x}^{(U)}$ generating $U{\hat{\phi }}_{x}{U}^{{\dagger} }$ such that ${\left\Vert {\phi }_{x}-{\hat{\phi }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le {c}^{{\prime} }\epsilon$ for all $x\in \tilde{X}$ and all U ∈ G.

• 4. Numerically solve the SDP shown in Proposition 1 by setting ρ = ϕ and ${\{{\hat{\rho }}_{x}\}}_{x\in \hat{X}}={\{U{\hat{\phi }}_{x}{U}^{{\dagger} }\}}_{x\in \tilde{X},U\in G}$ and obtain a probability distribution $\hat{p}$, which causes the approximation error δ-close to $\mathop{\min }\nolimits_{p}{\left\Vert \phi -{\sum }_{x\in \hat{X}}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}$.

• 5. Sample ${{{{\mathcal{C}}}}}_{x}^{(U)}$ in accordance with $\hat{p}$, whose domain is $\hat{X}=\tilde{X}\times G$.

The two properties can be verified as follows:

• Efficiency: We can verify that all steps of the algorithm take $poly\left(\log \left(\frac{1}{\epsilon }\right),\log \left(\frac{1}{\delta }\right)\right)$-time by using the following observations: We can construct a list ${\{{\phi }_{x}\}}_{x\in \tilde{X}}$ whose size is independent to ϵ. From the assumption on ${{{\mathcal{D}}}}$, we can also obtain a list of matrix representations of ${\{U{\phi }_{x}{U}^{{\dagger} }\}}_{x\in \tilde{X},U\in G}$ within $polylog\left(\frac{1}{\epsilon }\right)$-time. The ellipsoid method guarantees that the optimal value of our SDP can be computed in $poly\left(\log \left(\frac{1}{\epsilon }\right),\log \left(\frac{1}{\delta }\right)\right)$-time within an approximation error δ⁴⁴.

• Quadratic improvement: The minimum approximation error $\mathop{\min }\limits_{p}{\left\Vert \phi -{\sum }_{x\in \hat{X}}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}$ is at most ϵ² since ${\{{\hat{\rho }}_{x}\}}_{x\in \hat{X}}$ is a subset of an ϵ-covering ${\{{\hat{\rho }}_{x}\}}_{x\in \hat{X}}\cup {\{{\psi }_{y}\}}_{y}$ of S_G, where ${\{{\psi }_{y}\in {S}_{G}\}}_{y}$ is a finite ϵ-covering of $\{\psi \in {S}_{G}:{\left\Vert \phi -\psi \right\Vert }_{{{\mbox{tr}}}}\, > \,2\epsilon \}$ and ${\left\Vert \phi -{\psi }_{y}\right\Vert }_{{{\mbox{tr}}}}\, > \,2\epsilon$ for any y, ${\{{\hat{\rho }}_{x}\}}_{x\in \hat{X}}\cup {\{{\psi }_{y}\}}_{y}$ is invariant under the action of G, and we can thus apply Theorem 1 and Lemma 4.

  □

While this theorem assumes the dimension d of the Hilbert space is constant, we can also provide an estimation of the runtime of ${{{\mathcal{P}}}}$ when d grows. The runtime varies depending on the symmetry G that target states possess (see Supplementary Note 3). In the worst case where target states have no common symmetry, i.e., $G=\{{\mathbb{I}}\}$, the size of $\hat{X}$ will be $| \hat{X}| =poly(\exp (d))$. In this case, we can provide the upper bound on the runtime of ${{{\mathcal{P}}}}$ as $poly\left(\log \left(\frac{1}{\epsilon }\right),\log \left(\frac{1}{\delta }\right),\exp (d)\right)$-time, based on the proof of Theorem 2.

Numerical simulation of T-count reduction

In this section, we demonstrate how Theorem 2’s probabilistic synthesis algorithm can reduce the T-count through numerical simulation. We select a target state ϕ from ${S}_{G}=\{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{2}\right):\left\vert \phi \right\rangle =\cos t\left\vert 0\right\rangle +\sin t\left\vert 1\right\rangle ,t\in {\mathbb{R}}\}$, as shown in Fig. 1(b). Recall that S_G consists of G-invariant pure states, where $G=\{{\mathbb{I}},\theta \}$ with the complex conjugation θ.

We assume that the set of elementary gates consists of Clifford gates and T-gate, which is a commonly utilized gate set in FTQC based on stabilizer codes or surface codes. Considering that the implementation cost of a T-gate is much higher than that of Clifford gates, it is necessary to minimize the T-count of the circuits. To do this, we use the Ross-Selinger algorithm⁴⁵ to synthesize ${R}_{y}(2t)=\left(\begin{array}{rcl}\cos t&&-\sin t\\ \sin t&&\cos t\end{array}\right)$ and obtain a gate sequence that realizes a unitary operator U_t( ≃ R_y(2t)). This allows us to obtain an approximated state ${U}_{t}\left\vert 0\right\rangle (\simeq {R}_{y}(2t)\left\vert 0\right\rangle =\cos t\left\vert 0\right\rangle +\sin t\left\vert 1\right\rangle )$. Note that the Ross-Selinger algorithm can achieve an almost minimal T-count for synthesizing R_y(2t)⁴⁵. We run this deterministic synthesis algorithm for multiple randomly selected target states ϕ in S_G, with multiple target approximation errors. By utilizing the description of each output gate sequence, we determine the T-count and the actual approximation error.

We perform probabilistic synthesis based on Theorem 2 to synthesize the same multiple target states $\left\vert \phi \right\rangle$ with the same multiple target approximation errors. When the target approximation error is ϵ, we execute the Ross-Selinger algorithm within a target approximation error of $0.3\sqrt{\epsilon }$ for a $(0.7\sqrt{\epsilon })$-covering of $\{\psi \in {S}_{G}:{\left\Vert \psi -\phi \right\Vert }_{{{\mbox{tr}}}}\le 2\sqrt{\epsilon }\}$. A set consisting of the target state $\left\vert {\phi }_{1}\right\rangle =\cos t\left\vert 0\right\rangle +\sin t\left\vert 1\right\rangle$ and two shifted states ${\{\left\vert {\phi }_{x}\right\rangle \}}_{x = 2}^{3}=\{\cos {t}^{{\prime} }\left\vert 0\right\rangle +\sin {t}^{{\prime} }\left\vert 1\right\rangle :{t}^{{\prime} }=t\pm 2\arcsin (0.7\sqrt{\epsilon })\}$ forms such a $(0.7\sqrt{\epsilon })$-covering when ϵ ≤ 0.07. Thus, we obtain three gate sequences to generate states ${\{{\hat{\phi }}_{x}\}}_{x = 1}^{3}$ after executing the Ross-Selinger algorithm. To apply Theorem 2, we also require gate sequences to generate ${\{\theta {\hat{\phi }}_{x}\theta \}}_{x = 1}^{3}$, the complex conjugation of ${\{{\hat{\phi }}_{x}\}}_{x = 1}^{3}$. These gate sequences can be obtained by modifying the gate sequence to generate ${\hat{\phi }}_{x}$ without increasing the T-count. This is because θTθ ∝ ZST and the set of Clifford gates is closed under the complex conjugation. After obtaining six synthesized states ${\{{\hat{\phi }}_{x},\theta {\hat{\phi }}_{x}\theta \}}_{x = 1}^{3}$, we solve the SDP described in Proposition 1 to determine the actual approximation error. Theorem 2 guarantees the actual approximation error is smaller than ϵ. Note that without exploiting the symmetry of the target state, we need 13 states to form a $(0.7\sqrt{\epsilon })$-covering of $(2\sqrt{\epsilon })$-ball around ϕ due to the disk covering problem.

We examine how the T-count and the approximation error for a specific target state are related in Fig. 3. As we can see, we were able to achieve a 50 ~ 60% reduction in T-count. We observe similar behavior for other randomly selected target states (see https://github.com/akibue/prob-synthesisfor details).

Fig. 3: Relationship between T-count and the approximation error for synthesizing $\left\vert \phi \right\rangle =\cos t\left\vert 0\right\rangle +\sin t\left\vert 1\right\rangle$ with t = 1.

For each target approximation error, we run the Ross-Selinger algorithm to obtain a gate sequence to approximate ϕ. The blue dashed line interpolates points, each of which represents a target approximation error and the T-count of the gate sequence. The actual approximation error and the T-count achieved by the gate sequence are plotted by blue dots. Note that both the target and actual approximation errors are represented by ϵ. For each of the target approximation errors, we run the probabilistic synthesis algorithm and obtain a list of six gate sequences to be probabilistically sampled. The purple dashed line interpolates points, each of which represents a target approximation error and the maximum T-count of gate sequences in the list. The actual approximation error and the maximum T-count achieved by optimally mixing the gate sequence are plotted by purple dots.

Halving bit representation of pure states

We verify that the existence of probabilistic and deterministic encoding given in Fig. 2 can be reduced into a property of output states of the decoder Γ, as shown in the following propositions.

Proposition 2

A probabilistic encoding of ${{{\bf{P}}}}({{\mathbb{C}}}^{d})$ with approximation error ϵ and a label set X exists if and only if there exists set ${\{{\hat{\rho }}_{x}\in {{{\bf{S}}}}\left({{\mathbb{C}}}^{d}\right)\}}_{x\in X}$ of mixed states satisfying

$$\mathop{\max }\limits_{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)}\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon ,$$

(23)

where the minimization is taken over a probability distribution p over X.

Proposition 3

A deterministic encoding of ${{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)$ with approximation error ϵ and a label set X exists if and only if there exists set ${\{{\hat{\rho }}_{x}\in {{{\bf{S}}}}\left({{\mathbb{C}}}^{d}\right)\}}_{x\in X}$ of mixed states satisfying

$$\mathop{\max }\limits_{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)}\mathop{\min }\limits_{x\in X}{\left\Vert \phi -{\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}\le \epsilon .$$

(24)

A set ${\{{\hat{\rho }}_{x}\}}_{x\in X}$ of mixed states satisfying Eq. (24) is called an external ϵ-covering of ${{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)$. A set ${\{{\hat{\rho }}_{x}\in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)\}}_{x\in X}$ of pure states satisfying Eq. (24) is called an internal ϵ-covering of ${{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)$. The minimum size of internal (or external) ϵ-coverings is called the internal (or external) covering number and denoted by I_in (or I_ex). Note that I_ex ≤ I_in by definition and the minimum bit length ${n}_{\det }$ required for deterministic encodings is equal to $\lceil {\log }_{2}{I}_{{{{\rm{ex}}}}}\rceil$. We obtain the following lemma by using the volume consideration and applying the construction of an ϵ-covering shown in⁴².

Lemma 5

For any $\epsilon \in \left(0,\frac{1}{2}\right]$ and an integer d ≥ 2 specified below, the internal and external covering numbers I_in and I_ex of an ϵ-covering of ${{{\bf{P}}}}({{\mathbb{C}}}^{d})$ are bounded by

$$2\cdot l(d,2\epsilon )\le {\log }_{2}{I}_{{{{\rm{ex}}}}}\le {\log }_{2}{I}_{{{{\rm{in}}}}}\,\,\wedge \,\,2\cdot l(d,\epsilon )\le {\log }_{2}{I}_{{{{\rm{in}}}}}\le 2\cdot l(d,\epsilon )+{\log }_{2}(5d\ln d),$$

(25)

where $l(d,\epsilon ):= \left(d-1\right){\log }_{2}\left(\frac{1}{\epsilon }\right)$. Moreover, if d ≥ 4, the first lower bound can be strengthened as $2\cdot l(d,\epsilon )\le {\log }_{2}{I}_{{{{\rm{ex}}}}}$.

The details of the proof are given in Supplementary Note 4. By combining this lemma with Theorem 1, we obtain the following theorem about the minimum bit length.

Theorem 3

For any $\epsilon \in \left(0,\frac{1}{2}\right]$ and an integer d ≥ 2 specified below, the minimum bit length ${n}_{\det }$ (or n_prob) of the deterministic (or probabilistic) encoding of ${{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)$ with approximation error ϵ is bounded by

$$2\cdot l(d,2\epsilon )\le {n}_{\det }\le 2\cdot l(d,\epsilon )+{\log }_{2}(5d\ln d),$$

(26)

$$l(d,\epsilon )-{\log }_{2}d\le {n}_{{{{\rm{prob}}}}}\le l(d,\epsilon )+{\log }_{2}(5d\ln d),$$

(27)

where $l(d,\epsilon ):= \left(d-1\right){\log }_{2}\left(\frac{1}{\epsilon }\right)$. Moreover, if d ≥ 4, the first lower bound can be strengthened as $2\cdot l(d,\epsilon )\le {n}_{\det }$.

Proof

Since the bounds on ${n}_{\det }$ are a direct consequence of Lemma 5, we show the bounds on n_prob. The upper bound is obtained by setting ${\{{\hat{\rho }}_{x}\}}_{x}$ in Proposition 2 to be the minimum internal $\sqrt{\epsilon }$-covering of ${{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)$. This is because Theorem 1 with $G=\{{\mathbb{I}}\}$ guarantees that ${\{{\hat{\rho }}_{x}\}}_{x}$ satisfies Eq. (23), and an upper bound on the size of the internal $\sqrt{\epsilon }$-covering is given by Lemma 5.

Next, we show the lower bound on n_prob. Let ${\{{\hat{\rho }}_{x}\in {{{\bf{S}}}}({{\mathbb{C}}}^{d})\}}_{x\in X}$ satisfy Eq. (23). We obtain

$$\begin{array}{ll}\epsilon \,\ge \,\mathop{\max }\limits_{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)}\mathop{\min }\limits_{p}{\left\Vert \phi -\mathop{\sum}\limits_{x\in X}p(x){\hat{\rho }}_{x}\right\Vert }_{{{\mbox{tr}}}}\ge \mathop{\max }\limits_{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)}\mathop{\min }\limits_{p}\left(1-\mathop{\sum}\limits_{x}p(x)tr\left[\phi {\hat{\rho }}_{x}\right]\right)\\ \quad=\,1-\mathop{\min }\limits_{\phi \in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)}\mathop{\max }\limits_{x\in X}F\left({\hat{\rho }}_{x},\phi \right),\end{array}$$

(28)

where we use ${\left\Vert \rho -\sigma \right\Vert }_{{{\mbox{tr}}}}\ge \mathop{\max }\nolimits_{\phi \in {{{\bf{P}}}}\left({{{\mathcal{H}}}}\right)}tr\left[\phi (\rho -\sigma )\right]$ in the second inequality.

By letting ${\hat{\rho }}_{x}=\mathop{\sum }\nolimits_{i = 1}^{d}p(i| x){\phi }_{i| x}$, we ensure that for any $\phi \in {{{\bf{P}}}}({{\mathbb{C}}}^{d})$, there exists i and x such that

$$1-\epsilon \le F\left({\hat{\rho }}_{x},\phi \right)=\mathop{\sum }\limits_{j=1}^{d}p(j| x)F\left({\phi }_{j| x},\phi \right)\le F\left({\phi }_{i| x},\phi \right)=1-{\left\Vert \phi -{\phi }_{i| x}\right\Vert }_{\,{{\mbox{tr}}}\,}^{2}.$$

(29)

Thus, ${\{{\phi }_{i| x}\}}_{i,x}$ is an internal $\sqrt{\epsilon }$-covering of ${{{\bf{P}}}}({{\mathbb{C}}}^{d})$. Hence, the lower bound can be obtained by applying Lemma 5 as ${\log }_{2}(| X| d)\ge 2\cdot l(d,\sqrt{\epsilon })=l(d,\epsilon )$. □

Applications for analysis on entanglement measure

Determining whether a quantum state ρ is separable or entangled is a crucial inquiry in quantum information, as entanglement provides quantum advantages in various information processing tasks. The separability test is also fundamental to various optimization problems in distributed quantum computation. The separability test is computationally hard even if we are given the matrix representation of ρ⁴⁶. Further analysis of the computation complexity of the separability test has resulted in several important findings relating to QMA(2)^47,48,49,50. Although the separability test for general states is challenging, there are specific classes of states that make it easier to test for separability, e.g., low rank^51,52 and symmetric^53,54 states.

In order to identify the tractable states in the separability test, the study of the optimal convex approximation examines a generalized problem of how to approximate a target state ρ with a probabilistic mixture of a restricted subset ${\{{\hat{\rho }}_{x}\}}_{x}$ of quantum states^30,31,32. When this subset consists of product states, it becomes the separability test. From this general perspective, we demonstrated that restricting a target state to be rank-one or symmetry simplifies the optimization, as shown in Lemma 3. Furthermore, we demonstrate that our general lemma for the optimal convex approximation can reproduce the nontrivial facts about entanglement, either already known or derivable through known facts, in a simpler and unified way.

Recall that the set of separable states is defined as follows.

Definition 1

${{{\bf{SEP}}}}:= \{\sigma \in {{{\bf{S}}}}\left({{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d}\right):\sigma ={\sum }_{x}p(x){\phi }_{x}\otimes {\psi }_{x}\wedge {\phi }_{x},{\psi }_{x}\in {{{\bf{P}}}}\left({{\mathbb{C}}}^{d}\right)\}$.

In³³, Girardin et al. used a neural network to conjecture Eqs. (2). Recall that ${\rho }_{q}^{{{{\rm{WER}}}}}\in {{{\bf{S}}}}({{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d})$ is the Werner state defined as ${\rho }_{q}^{{{{\rm{WER}}}}}:= \frac{2(1-q)}{d(d+1)}{\Pi }_{\vee }+\frac{2q}{d(d-1)}{\Pi }_{\wedge }$ with Hermitian projectors Π_∨ and Π_∧ whose ranges are the symmetric subspace and antisymmetric subspace and ${\rho }_{q}^{{{{\rm{ISO}}}}}\in {{{\bf{S}}}}({{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d})$ is the isotropic state defined as ${\rho }_{q}^{{{{\rm{ISO}}}}}:= \frac{1-q}{{d}^{2}}{\mathbb{I}}+q{\Phi }^{+}$ with $\left\vert {\Phi }^{+}\right\rangle =\frac{1}{\sqrt{d}}\mathop{\sum }\nolimits_{i = 0}^{d-1}\left\vert ii\right\rangle$, respectively. Since the Werner (or isotropic) state is entangled if and only if $\frac{1}{2}\, < \,q\le 1$ (or $\frac{1}{d+1}\, < \,q\le 1$), we assume they are entangled in Eqs. (2). By exploiting the symmetry of the Werner (or isotropic) state and using Lemma 3, we can prove this conjecture. The complete proof is given in Supplementary Note 5.

Note that Eqs. (2) can be proven straightforwardly by combining the following two facts: (i) the closest separable state can be assumed to be the Werner (or isotropic) state without loss of generality, and (ii) the Werner (or isotropic) state is separable if and only if $0\le q\le \frac{1}{2}$ (or $-\frac{1}{{d}^{2}-1}\le q\le \frac{1}{d+1}$). In contrast, our proof directly computes the minimum trace distance without constructing the closest separable state, moreover, it includes a proof for (ii). Since a POVM element M appeared in Eq. (8) can be regarded as an entanglement witness, our proof can be regarded as a method for “quantifying entanglement with witness operators”^55,56. Taking account of the fact that the closest separable state is not necessary in our method, it is expected that the advantage of our method becomes obvious when the closest separable state is unknown or analytically hard to obtain, as shown in the next example.

Due to its clear operational meaning, the resource measure based on trace distance has been investigated for various resource theories, including entanglement and coherence⁵⁷. Lemma 3 provides an alternate concise proof for the following recently identified coincidence between entanglement and coherence measures.

Proposition 4

(³⁴, Theorem 3) For pure states $\left\vert \Phi \right\rangle =\mathop{\sum }\nolimits_{i = 0}^{d-1}{\alpha }_{i}\left\vert ii\right\rangle$ and $\left\vert \phi \right\rangle =\mathop{\sum }\nolimits_{i = 0}^{d-1}{\alpha }_{i}\left\vert i\right\rangle$, it holds that

$$\mathop{\min }\limits_{\sigma \in {{{\bf{SEP}}}}}{\left\Vert \Phi -\sigma \right\Vert }_{{{\mbox{tr}}}}=\mathop{\min }\limits_{\rho \in I}{\left\Vert \phi -\rho \right\Vert }_{{{\mbox{tr}}}},$$

(30)

where $I:= \,{{\mbox{conv}}}\,\left({\{\left\vert i\right\rangle \left\langle i\right\vert \}}_{i = 0}^{d-1}\right)$ is called a set of incoherent states and ${\{\left\vert i\right\rangle \}}_{i = 0}^{d-1}$ is an orthonormal basis.

Since it is suggested that a simple closed-form formula for Eq. (30) might not exist³⁴, the closest separable state is also hard to obtain. However, our method is applicable to show the relationship of the minimum approximation error between different types of probabilistic approximation by exploiting the purity of the target states. Moreover, it simplifies the proof of^{34,Theorem 3]}. The complete proof is given in Supplementary Note 5.

Discussion

We investigated the limitation of the optimal probabilistic state synthesis and its potential for reducing the size of a synthesis circuit. As a main result, we verified the tight relationship between the approximation error obtained by the optimal probabilistic state synthesis and the optimal deterministic one. We also constructed an efficient method to convert a deterministic synthesis algorithm into a probabilistic one that quadratically reduces the approximation error.

To estimate how the error reduction reduces the size of a synthesis circuit, we performed a numerical simulation and evaluated the length of the classical bit string required to approximately encode a pure state. As a result, we found that probabilistic encoding asymptotically halves the bit length. Note that under the presence of noise on elementary gates, which was not taken into account in this study, certain conditions on the noise may be required to achieve the quadratic reduction of the approximation error. However, our SDP can still be used to numerically determine the optimal probabilistic synthesis in cases where the noise is explicitly described.

In addition to our contribution to the state synthesis, the our result would improve the performance of classical simulation of a quantum computer as well as that of optimization algorithms including a brute force search over pure states, e.g., the separability test⁵⁸. This is because we essentially show that the set of pure states can be approximated by its ϵ-covering or probabilistic mixtures of its $\sqrt{\epsilon }$-covering in the same accuracy, where the size of the minimum $\sqrt{\epsilon }$-covering is almost the square root of that of the minimum ϵ-covering.

These results are based on general theorems about the optimal convex approximation of a quantum state. While the optimal convex approximation and state synthesis have been studied in different contexts, our theorems have demonstrated that analyzing the former problem provides not only the fundamental limitation of probabilistic synthesis but also a construction of an efficient synthesis algorithm. Furthermore, our theorems contribute to the original motivation of the studies of the optimal convex approximation^30,31,32, which is quantifying a resource measure in convex resource theories^59,60,61 such as the resource theory of entanglement. Indeed, the SDP constructed in Proposition 1 would provide a basis for numerical investigation for such resource measures. Our theorems would reveal more quantitative relationships between different resource measures as shown in Proposition 4.