Reflection and Transmission of Inhomogeneous Plane Waves in Thermoporoelastic Media

Abstract

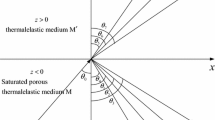
We study the reflection and transmission (R/T) characteristics of inhomogeneous plane waves at the interface between two dissimilar fluid-saturated thermoporoelastic media at arbitrary incidence angles. The R/T behaviors are formulated based on the classic Lord–Shulman (LS) and Green–Lindsay (GL) heat-transfer models as well as a generalized LS model, respectively. The latter results from different values of the Maxwell-Vernotte-Cattaneo relaxation times. These thermoporoelastic models can predict three inhomogeneous longitudinal (P1, P2, and T) waves and one shear (S) wave. We first compare the LS and GL models for the phase velocities and attenuation coefficients of plane waves, where the homogeneous wave has a higher velocity but weaker thermal attenuation than the inhomogeneous wave. Considering the oil–water contact, we investigate R/T coefficients associated with phase angles and energy ratios, which are formulated in terms of incidence and inhomogeneity angles, with the latter having a significant effect on the interference energy. The proposed thermoporoelastic R/T model predicts different energy partitions between the P and S modes, especially at the critical angle and near grazing incidence. We observe the anomalous behavior for an incident P wave with the inhomogeneity angle near the grazing incidence. The energy partition at the critical angle is mainly controlled by relaxation times and boundary conditions. Beyond the critical angle, the energy flux predicted by the Biot poroelastic and LS models vanishes vertically, becoming the opposite for the GL and generalized LS models. The resulting energy flux shows a good agreement with the R/T coefficients, and they are well proven by the conservation of energy, where the results are valuable for the exploration of thermal reservoirs.

Appendix A

The constitutive relations for the stress $\sigma _{ij}$, strain $\epsilon _{ij}$ and fluid pressure p of thermoporoelasticity can be expressed as follows (Wang et al. 2021):

$$\begin{aligned} \begin{aligned}&\sigma _{ij}=2\mu \epsilon _{ij}+[\lambda \epsilon _{m}+\bar{\alpha }M\epsilon -\beta (T+\tau _1\dot{T})]\delta _{ij}, \\&-p=M\epsilon -\frac{\beta _{f}}{\bar{\phi }}( T+\tau _2\dot{T} ), \\&\epsilon =\bar{\alpha }\epsilon _{m}+\epsilon _{f},\ \ \ \epsilon _{m}=u_{i,i},\ \ \ \epsilon _{f}=w_{i,i},\ \ \ 2\epsilon _{ij}=u_{i,j}+u_{j,i}, \\ \end{aligned} \end{aligned}$$

(A.1)

where $\delta _{ij}$ is the Kronecker function. The equations of momentum conservation are

$$\begin{aligned} \begin{aligned}&\sigma _{ij,j}=\rho \ddot{u}_i+\rho _f\ddot{w}_i, \\&-p_{,i}=\rho _f\ddot{u}_i+m\ddot{w}_i+\displaystyle \frac{\eta }{\bar{\kappa }}\dot{w}_i. \end{aligned} \end{aligned}$$

(A.2)

Substituting the stress–strain relation (Eq. (A.1)) into the equations of momentum conservation (Eq. (A.2)) and strain–displacement relations, we obtain compact equations for displacement components

$$\begin{aligned} \begin{aligned}&(\lambda +\mu +{\bar{\alpha }}^2M)u_{j,ji}+\mu u_{i,jj}+\bar{\alpha }Mw_{j,ji}-\beta (T_{,i}+\tau _1\dot{T}_{,i}) =\rho \ddot{u}_i+\rho _f\ddot{w}_i, \ \ \ i,j =x,y,z, \\&\bar{\alpha }Mu_{j,ji}+Mw_{j,ji}-\displaystyle \frac{\beta _f}{\bar{\phi }}(T_{,i}+\tau _2\dot{T}_{,i}) =\rho _f\ddot{u}_i+m\ddot{w}_i+\displaystyle \frac{\eta }{\bar{\kappa }}\dot{w}_i. \\ \end{aligned} \end{aligned}$$

(A.3)