Fast Computation of Terrain-Induced Gravitational and Magnetic Effects on Arbitrary Undulating Surfaces

Abstract

Based on a brief review of forward algorithms for the computation of topographic gravitational and magnetic effects, including spatial, spectral and hybrid-domain algorithms working in either Cartesian or spherical coordinate systems, we introduce a new algorithm, namely the CP-FFT algorithm, for fast computation of terrain-induced gravitational and magnetic effects on arbitrary undulating surfaces. The CP-FFT algorithm, working in the hybrid spatial-spectral domain, is based on a combination of CANDECOMP/PARAFAC (CP) tensor decomposition of gravitational integral kernels and 2D Fast Fourier Transform (FFT) evaluation of discrete convolutions. By replacing the binomial expansion in classical FFT-based terrain correction algorithms using CP decomposition, convergence of the outer-zone computation can be achieved with significantly reduced inner-zone radius. Additionally, a Gaussian quadrature mass line model is introduced to accelerate the computation of the inner zone effect. We validate our algorithm by computing the gravitational potential, the gravitational vector, the gravity gradient tensor, and magnetic fields caused by densely-sampled topographic and bathymetric digital elevation models of selected mountainous areas around the globe. Both constant and variable density/magnetization models, with computation surfaces on, above and below the topography are considered. Comparisons between our new method and space-domain rigorous solutions show that with modeling errors well below existing instrumentation error levels, the calculation speed is accelerated thousands of times in all numerical tests. We release a set of open-source code written in MATLAB language to meet the needs of geodesists and geophysicists in related fields to carry out more efficiently topographic modeling in Cartesian coordinates under planar approximation.

Article Highlights

• A new algorithm is presented for the efficient computation of terrain-induced gravitational and magnetic fields on arbitrary surfaces

• Tensor decomposition instead of the classical binomial expansion is used to achieve optimal approximations of the integral kernel functions

• The new method is validated by comparing with space-domain rigorous solutions using various densely-sampled digital elevation models

1 Introduction

The calculation of the gravitational potential (GP), the gravitational vector (GV), the gravity gradient tensor (GGT), and magnetic fields on a surface describing the measurement positions from varying terrain with constant or variable density/magnetization is a classical problem in geophysics and geodesy (Pedersen et al. 2015). In geophysical study, for ground-based, airborne or near-seabed measurements, observations are made on an undulating surface above the local topography or bathymetry. Therefore, it is desirable to remove terrain-induced gravitational and magnetic effects from observed data in order to isolate the anomalies to be investigated (Plouff 1976; Grauch 1987; Hildenbrand et al. 1993; Bouligand et al. 2014), or to interpret the anomalous sources that contain the terrain as a whole (Parker and Huestis 1974; Macdonald et al. 1983; Tontini et al. 2008; Searle et al. 2019). In both cases, an efficient algorithm for computing topographic gravitational and magnetic effects on arbitrary undulating surfaces plays a central role.

In geodesy, topographic global gravity field models of the Earth (Grombein et al. 2016; Rexer et al. 2016; Ince et al. 2020), obtained by forward calculation of the gravity effect caused by some global topographic models, such as the 1 arc-sec resolution Earth2014 model (Hirt and Rexer 2015), are organized and updated at the International Centre for Global Earth Models (ICGEM) (Ince et al. 2019). They are useful in spectral augmentation of global gravity models based on satellite and terrestrial gravity measurements (Hirt et al. 2013; Rexer 2017; Zingerle et al. 2020; Ince et al. 2020), in filling the gaps where actual gravity observations are limited or unavailable (Pavlis et al. 2012), and also in deriving global Bouguer and isostatic gravity anomaly maps (Balmino et al. 2012).

Generally speaking, there are three major algorithms for computing terrain-induced gravitational and magnetic fields, including space-domain (or spatial-domain) algorithms, spectral-domain algorithms (sometimes called Fourier-domain algorithms in local studies under planar approximation), and hybrid space-spectral domain algorithms. Each of them can be further subdivided into several different types according to the specific forward computation required in either local, regional or global modeling.

Space-domain algorithms are based on the superposition principle of gravitational and magnetic fields. Usually the topographic source is decomposed into a bunch of mass elements, including polyhedron (Werner and Scheeres 1997; Holstein 2003; Jekeli and Zhu 2006; Tsoulis 2012; D’Urso and Trotta 2017; Ren et al. 2018; Zhang and Chen 2018; Holzrichter et al. 2019; Saraswati et al. 2019), rectangular prism (Bhattacharyya 1964; Nagy et al. 2000; Garcia-Abdeslem 2005; Jiang et al. 2018; Karcol 2018; Fukushima 2020), spherical/spheroidal/ellipsoidal prism (tesseroid) (Asgharzadeh et al. 2007; Du et al. 2015; Roussel et al. 2015; Baykiev et al. 2016; Grombein et al. 2016; Uieda et al. 2016; Deng and Shen 2018; Fukushima 2018; Lin et al. 2020), mass line and mass point (Heck and Seitz 2007; Wild-Pfeiffer 2008), and the contributions for each element are calculated and summed together. Depending on the attenuation character of Newton’s integral kernel with distance, it is numerically more advantageous to use a combination of multiple mass elements for forward simulation than to use a single one. Simpler mass elements, such as the mass line and mass point, accompanied usually by DEMs with reduced spatial resolution, can be applied for far-zone effect computation to accelerate the forward process. More complex elements, such as the polyhedron and the rectangular prism, accompanied by high-resolution DEMs, provide more accurate near-zone effect which are critical to maintain the high frequency part of the true results (Tsoulis et al. 2009; Cella 2015; Benedek et al. 2018; Hirt et al. 2019; Yang et al. 2020). Although GPU and parallel programming techniques can be applied to improve the speed of computation (Moorkamp et al. 2010; Zhang et al. 2015), space-domain algorithms are still computationally expensive for forward modeling over large areas using detailed DEMs.

Spectral-domain algorithms refer to Fast Fourier Transform (FFT) based algorithms for local terrain modeling in Cartesian coordinate system, and spherical harmonic transform (SHT) based algorithms for global modeling in spherical coordinate system. The former, to which this work is closely related, shall be discussed later. The latter, when applied for the modeling of gravitational and magnetic fields on a sphere (with constant radius) due to finite amplitude topography, can be understood as the spherical analog to the Cartesian result of Parker (1973). This algorithm and its extensions have been extensively used in calculating topographic gravitational field models caused by terrestrial planets (Rummel et al. 1988; Martinec et al. 1989; Balmino 1994; Wieczorek and Phillips 1998; Ramillien 2002; Featherstone et al. 2013; Hirt and Kuhn 2014; Tenzer et al. 2015; Wieczorek 2015; Sprlak et al. 2018; Ince et al. 2020). By combining with upward and downward continuation techniques, the algorithm can also be extended to the computation of gravitational fields on the rugged surfaces of planetary bodies (Balmino et al. 2012; Hirt 2012; Bucha and Janák 2014; Rexer et al. 2016; Bucha et al. 2019b).

Despite its popularity in topographic potential modeling, it has been proved mathematically that regardless of the smoothness of the density and topography, spherical harmonic series converges exactly in the closure of the exterior of the Brillouin sphere, and convergence below the Brillouin sphere occurs with probability zero (Costin et al. 2022). A great many recent numerical experiments also support this conclusion (Hirt and Kuhn 2017; Bucha and Sansò 2021; Sprlak and Han 2021). Divergence of the series occurs at higher degrees for large-sized, near-spherical planets such as the Earth and the Moon, but may occur at much lower degrees for medium and small-sized, non-spherical, irregularly shaped asteroids, comets and moons (Hu and Jekeli 2015; Reimond and Baur 2016; Bucha and Sansò 2021). Convergence behavior can be improved, especially for computation points lie between the Brillouin sphere and the Brillouin spheroid/ellipsoid, by applying spheroidal/ellipsoidal harmonic series instead (Garmier et al. 2002; Claessens and Hirt 2013; Wang and Yang 2013; Rexer et al. 2016; Sprlak et al. 2020). However, this does not fundamentally change the divergent nature of the series. Alternatively, a combination of external/internal spherical harmonic series expansions may be a feasible scheme (Górski et al. 2018; Bucha and Sansò 2021; Sprlak and Han 2021), but still adds lots of additional computation spheres, each with a different set of harmonic coefficients, and extra interpolation when forward results are required on an arbitrary undulating surface.

Hybrid space-spectral domain algorithms, compared with the previous two, have better performance in balancing the contradiction between numerical accuracy and efficiency. They rely on a combination of FFT/SHT and space-domain rigorous formula in solving local/global terrain modeling problems, respectively. The FFT-based hybrid algorithm, to which this work belongs, shall be discussed in detail later. To implement the SHT-based hybrid algorithm for global terrain modeling, as far as we know, there are two approaches. One is to decompose the topography using the residual terrain modeling (RTM) technique (Hirt et al. 2019), the other is to modify Newton’s integral kernel within a certain spherical distance (Bucha et al. 2019a; Bucha and Kuhn 2020). The essential idea of both two methods is to decompose the target forward field into two parts, one of which contains only low frequency (long-wavelength) constituents. Since gravitational computation can be expressed as the convolution of the DEM and Newton’s integral kernel, this can be done either by using a low-pass filtered DEM (e.g., the RTM technique) (Hirt et al. 2019), or a modified band-limited convolution kernel (Bucha et al. 2019a). In this way, divergence of the spherical harmonic series can be controlled within acceptable limits even at the planet’s surface. The residual terrain, or the near-zone effects, which contain extremely rich high-frequency components, are evaluated rigorously by some space-domain solutions, such as the polyhedron or the rectangular prism. Since the space-domain evaluation is required only within a certain spherical distance for each computation point, the speed advantage of spectral domain method can be well preserved. Reported values for the space-domain integration radius are about 15 km for the Moon (Bucha and Kuhn 2020), and 40 km for the Earth (Hirt et al. 2019), these may be sufficient for global modeling using low-resolution DEMs, but are still computationally too expensive for local terrain modeling with high-resolution DEMs.

FFT-based algorithms, to which this work belongs, are suitable for topographic modeling in Cartesian coordinates under planar approximation. To our knowledge, there are four types of FFT-based algorithms applicable for the computation of terrain-induced gravity or magnetic fields on an undulating surface. Two of them based on 2D FFT, and the other two on 3D FFT, depending on whether the analytical or the discrete kernel spectrum is used (Sanso and Sideris 2013, page 462):

• 1. The first 2D FFT algorithm is a simple extension of Parker’s method using the analytical kernel spectrum (Parker 1973). By combining forward modeling on a horizontal plane above the topography and downward continuation using Taylor series expansion, forward results on a draped surface can be calculated efficiently (Pedersen et al. 2015; Wu 2021). However, in this way only a low-pass filtered version of the true terrain effect can be obtained due to the unstable downward continuation process.

• 2. The second 2D FFT algorithm, which is based on the discrete kernel spectrum and binomial expansion (Forsberg 1984, 1985), is more popular in geodetic studies for computing gravimetric terrain corrections. FFT here no longer serves as the numerical counterpart (rectangle or trapezoidal quadrature rule) of the continuous Fourier transform, but as a tool for the accurate evaluation of Toeplitz matrix–vector multiplications after embedding into a circulant matrix–vector multiplication system (Wu 2018). Despite that this algorithm has been studied and improved by many authors, it still requires a large part of space-domain computation to ensure convergence of the spectral part due to the limitation of using binomial expansions (Sideris 1984; Li and Sideris 1994; Martinec et al. 1996; Parker 1996; Tsoulis 2001; Goyal et al. 2020).

• 3. Analogously, the first 3D FFT algorithm is to use the 3D analytical spectrum of the Newton’s kernel (Tontini et al. 2009). The topographic source is first decomposed into a 3D grid of rectangular prisms, after which 3D FFTs are applied to calculate gravity or magnetic fields also on a 3D regular grid. Forward values on arbitrary surfaces can be obtained through interpolation. The method suffers from spectral leakage and truncation errors (Wu and Tian 2014). Improved version of the algorithm is introduced in Zhao et al. (2018) based on the Gauss-FFT algorithm (Wu 2016).

• 4. The second 3D FFT algorithm, which is based on the discrete kernel spectrum, applies 3D FFTs to evaluate 3D discrete convolutions (Sanso and Sideris 2013, page 468, 473). The zero-padding technique applied to eliminate edge effects is in fact mathematically equivalent to the Toeplitz-circulant matrix embedding process (Zhang and Wong 2015; Wu 2018; Chen and Liu 2019; Hogue et al. 2020; Vatankhah et al. 2022). The advantage of using a 3D FFT algorithm is that 3D variable density or magnetization can be incorporated easily. However, since regular 3D grids are used both in decomposing the topographic source and in defining computation coordinates, and topographic or observation height values are somehow arbitrary, usually it requires a very small grid step in the vertical direction (e.g., 5 m or even less) to guarantee the modeling accuracy at the expense of increased storage and computational efforts.

In this study, we introduce a CP-FFT algorithm, a new hybrid spatial-spectral domain algorithm working in Cartesian coordinates, for fast and accurate computation of terrain-induced gravitational and magnetic effects on arbitrary undulating surfaces. We start by analyzing the key idea of the classical FFT-based terrain correction algorithm, based on which we make a significant step by embedding the CP tensor decomposition into the approximation of the terrain correction convolution kernel. Next we extend our new method to all gravitational components commonly applied, and to magnetic field modeling through the Poisson’s relation. Finally, we test our algorithm using topographic and bathymetric datasets around the globe by comparing to space-domain rigorous solutions. We release a set of open source codes written in MATLAB language to scientists working in a related field.

2 Algorithm Formulations

2.1 The Classical Terrain Correction Algorithm

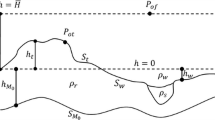
We denote $\varvec{r}=(x,y,z)$ as the computation point, $\varvec{\tilde{r}}=(\tilde{x},\tilde{y},\tilde{z})$ as the running integration point, and $R=\vert \varvec{r}-\varvec{\tilde{r}}\vert$ is the Euclidean distance between the computation and the integration point. The coordinate system is chosen with positive x pointing north, positive y pointing east, and positive z pointing downward. Suppose we have the topographic height function $\tilde{z}=h(\tilde{x},\tilde{y})$, the computation required on an undulating surface $z=H(x,y)$, the integration is carried out over the rectangular area $\Omega =[X1,X2] \times [Y1,Y2]$, with topographic masses outside this region ignored, then the gravitational terrain correction can be written as (Goyal et al. 2020):

$$\begin{aligned} g_{z}^{{tc}} (x,y,H) = & \;G\rho \int_{{Y1}}^{{Y2}} {\int_{{X1}}^{{X2}} {\int_{H}^{h} {\frac{\partial }{{\partial z}}} } } \left( {\frac{1}{R}} \right)d\tilde{x}d\tilde{y}d\tilde{z} \\ = & \;G\rho \int_{{Y1}}^{{Y2}} {\int_{{X1}}^{{X2}} {\left( {\frac{1}{L}\left[ {1 - \left( {1 + \left( {\frac{{H - h}}{L}} \right)^{2} } \right)^{{ - \frac{1}{2}}} } \right]} \right)} } d\tilde{x}d\tilde{y}, \\ \end{aligned}$$

(1)

where G is Newton’s gravitational constant, $\rho$ is the constant topographic density, and $L=\sqrt{(x-\tilde{x})^2+(y-\tilde{y})^2}$ is the planar Euclidean distance.

By expanding the term $\left[ 1+\left( \frac{H-h}{L}\right) ^2\right] ^{-\frac{1}{2}}$ into a binomial series according to

$$\begin{aligned} (1+x)^{-\frac{1}{2}}\approx \sum _{n=0}^{N_{B}}(-1)^{n}\frac{(2n-1)!!}{(2n) !!}x^n =1-\frac{1}{2}x+\frac{1\cdot 3}{2\cdot 4}x^2-\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}x^3+\cdots , \end{aligned}$$

(2)

with $N_{B}$ the order of expansion, we have:

$$\begin{aligned} g_{z}^{tc}(x,y,H) \approx G\rho \int _{Y1}^{Y2}\int _{X1}^{X2} \left[ \frac{(H-h)^2}{2 L^3}-\frac{3 (H-h)^4}{8 L^5}+\frac{15 (H-h)^6}{48 L^7} -\cdots \right] d\tilde{x} d\tilde{y}, \end{aligned}$$

(3)

in which the variables L, H and h can be separated, recasting the expression into a weighted summation of a series of continuous convolutions:

$$\begin{aligned} g_{z}^{tc}(x,y,H) \approx G\rho \sum _{(i_1,i_2,i_3)} \omega _{(i_1,i_2,i_3)} H^{i_1} \left( h^{i_2} * L^{-i_3}\right) , \end{aligned}$$

(4)

with $(i_1,i_2,i_3)$ representing all combinations of integer powers of H, h and L after Eq. 3 is full expanded, $\omega _{(i_1,i_2,i_3)}$ the corresponding coefficients, and the symbol $*$ indicating continuous convolutions of two functions.

After discretizing the integration region $\Omega$ using a regular grid of mass line or mass prism elements, the continuous convolution-type integrals reduce to discrete convolutions (Li and Sideris 1994), which can then be evaluated accurately and efficiently by combining circulant embedding of Toeplitz matrix–vector multiplications with FFT-based algorithms (Vogel 2002; Zhang and Wong 2015; Wu 2018; Chen and Liu 2019).

Although this binomial expansion method works perfectly well for a mildly varying topography, it has been clearly demonstrated in many previous works that its convergence depends strictly on the condition $\left| \frac{H-h}{L}\right| \le 1$ (Tsoulis 2001; Goyal et al. 2020), meaning that the slope of every line connecting a computation point and an integration point should not exceed $45^{\circ }$, which is a strong restriction that can be easily violated by steeply varying topographic models in most mountainous areas of the Earth.

Denoting the integral kernel function in Eq. 1 as:

$$\begin{aligned} \mathcal {K}_{g_z}^{tc}(L,H,h)=\frac{1}{L}-\frac{1}{\sqrt{L^2+(H-h)^2}}, \end{aligned}$$

(5)

the divergence problem has been partially solved by using a separating radius $R_{FFT}$ to divide the terrain correction integration into two zones (Tsoulis 2001; Goyal et al. 2020):

$$\begin{aligned} g_{z}^{{tc}} (x,y,H) = & \;\hat{g}_{z}^{{tc}} (x,y,H) + \bar{g}_{z}^{{tc}} (x,y,H) \\ = & \;G\rho \iint {_{{L < R_{{FFT}} }} {\mathcal{K}}_{{g_{z} }}^{{tc}} d\tilde{x}d\tilde{y} + G\rho }\iint_{{L \ge R_{{FFT}} }} {{\mathcal{K}}_{{g_{z} }}^{{tc}} }d\tilde{x}d\tilde{y}, \\ \end{aligned}$$

(6)

with the inner zone effect $\hat{g}_{z}^{tc}$ computed using space-domain rigorous solutions, and the outer zone effect $\bar{g}_{z}^{tc}$ evaluated using the FFT-based procedure described above. However, there remain unresolved issues with this combined approach: (1) to ensure convergence, usually a large radius $R_{FFT}$ is required, leading to time-consuming evaluation of the inner zone effect using space-domain solutions; (2) the algorithm is designed only for the $g_z$ component, whether it can be effectively extended to the forward modeling of other GP, GV, GGT components and magnetic fields still needs further investigations. These problems become particularly prominent when various gravitational and magnetic components are required from large-scale, high-resolution topographic or bathymetric models. In the following, we introduce a new CP-FFT method to overcome these deficiencies.

2.2 Improved Terrain Correction Algorithm Using CP Tensor Decomposition

The key idea behind terrain correction computation is the approximation of the integral kernel $\mathcal {K}_{g_z}^{tc}(L,H,h)$ using a summation of products of single-variable functions A(L), B(H) and C(h). Taylor series expansions (including the binomial expansion), even with optimally chosen parameters (Li and Sideris 1994), have been proved invalid in mountainous areas when densely-sampled DEMs (e.g., $<100$ m resolution) are used (Tsoulis 2001; Goyal et al. 2020). Combining space-domain solution to evaluate a circular region surrounding each computation point with a large radius ($R_{FFT}$) will slow down the entire process significantly. Here we introduce an alternative approach based on CANDECOMP/PARAFAC (CP) tensor decomposition of the terrain correction kernel function.

Fig. 1

a Illustration of the CP decomposition of the 3D kernel function $\mathcal {K}_{g_z}^{tc}(L,H,h)$ (redrawn from Kolda and Bader 2009, Fig. 3.1). The function $\mathcal {K}_{g_z}^{tc}$ is approximated using both CP decomposition of rank $N_{CP}=50$ ($N_L=N_H=N_h=100$) and binomial series of order $N_{B}=6$ (with 48 terms) in the region of interest $[L,H,h] \in [1,300] \times [0,10] \times [0,10]$ km$^3$. The 3D true function values are shown in b (in $\log _{10}\vert \mathcal {K}_{g_z}^{tc}\vert$ scale), with errors ($\log _{10}\vert \delta \vert$) of the CP decomposition and binomial series shown in c and d, respectively. The 1D true function values are shown in e by choosing a fixed value of $H=2$ km and 6 different values of $L \in [1,300]$ km. The corresponding errors for CP decomposition and binomial series are shown in f and g, respectively

As shown in Fig. 1a, first the 3D kernel function $\mathcal {K}_{g_z}^{tc}(L,H,h)$ is sampled on a rectilinear grid covering the region of interest:

$$\begin{aligned} (L,H,h)\in [L_\mathrm{{min}},L_\mathrm{{max}}] \times [H_\mathrm{{min}},H_\mathrm{{max}}] \times [h_\mathrm{{min}},h_\mathrm{{max}}], \end{aligned}$$

(7)

with:

$$\begin{aligned} L_i= & {} L_{min} s^{i-1}, \quad i=1,2,\cdots ,N_L, \nonumber \\ H_j= & {} H_{min}+(j-1) \Delta H, \quad j=1,2,\cdots ,N_H, \nonumber \\ h_k= & {} h_{min}+(k-1) \Delta h, \quad k=1,2,\cdots ,N_h, \end{aligned}$$

(8)

whereas $s=\frac{L_\mathrm{{max}}}{L_\mathrm{{min}}}^{\frac{1}{N_L-1}}$ is the common ratio of the geometric sequence $L_i$, and $\Delta H=\frac{H_\mathrm{{max}}-H_\mathrm{{min}}}{N_{H}-1}$, $\Delta h=\frac{h_\mathrm{{max}}-h_\mathrm{{min}}}{N_{h}-1}$ are the common differences of the arithmetic sequences $H_j$ and $h_k$, respectively. A geometric sampling (linear sampling in the $\log$ space) is used for the L variable considering the rapid decay of the kernel function with respect to increasing distance between the source and the computation point.

Next the 3D array $\mathcal {K}_{g_z}^{tc}(L_i,H_j,h_k)$ obtained from discrete sampling is approximated using CP decomposition of rank $N_{CP}$ as (see Fig. 1a):

$$\begin{aligned} \mathcal {K}_{g_z}^{tc}(L_i,H_j,h_k) \approx \sum _{n=1}^{N_{CP}}\lambda _n A_n(L_i)B_n(H_j)C_n(h_k), \end{aligned}$$

(9)

then function values $\mathcal {K}_{g_z}^{tc}(L,H,h)$ at an arbitrary position within the region of interest can be obtained through a simple linear interpolation. Note that the linear interpolation is implemented in the $\log$ space for the L variable for improved numerical accuracy.

The function cp_als in the MATLAB Tensor Toolbox (Brett et al. 2021), which computes an estimate of the best rank-N CP model of a tensor using the well-known alternating least-squares algorithm (Kolda and Bader 2009), is used to obtain a discrete approximation of our kernel function. Figure 1 compares approximation errors by using CP tensor decomposition of rank 50 (Fig. 1c, f) and those from binomial expansion of order 6 with 48 terms (Fig. 1d, g) in a region of interest $[L,H,h] \in [1,300] \times [0,10] \times [0,10]$ km$^3$, representing a typical $2^{\circ } \times 2^{\circ }$ DEM dataset of the most mountainous area on the Earth. A small separating radius $R_{FFT}=1$ km is applied. It can be clearly observed that while the binomial expansion fails when $\left| \frac{H-h}{L}\right| > 1$, with errors well above the $10^{0}$ level, the CP decomposition has errors below the $10^{-2}$ level in the entire region of interest.

Applying the CP decomposition, we have the outer zone effect reformulated as:

$$\begin{aligned} \bar{g}_{z}^{tc}(x,y,H) \approx G\rho \sum _{n=1}^{N_{CP}} \lambda _n B_n(H) \left[ C_n(h) * A_n(L) \right] , \end{aligned}$$

(10)

with the convolution-type integrals $C_n(h) * A_n(L)$ evaluated efficiently using FFTs, $A_n(L)$ set to zero when $L<R_{FFT}$, and $B_n(H)$ moved outside the convolution integral since it is a simple function of computation coordinates (x, y). In this way, convergence can be guaranteed even for a small separating radius $R_{FFT}$, which greatly speeds up the calculation of the inner zone effect using space-domain solutions. We call this new approach the CP-FFT algorithm.

2.3 CP-FFT for GP, GV, GGT Components with Laterally Variable Density

The CP-FFT algorithm can be easily extended to other gravitational components, and to the case of laterally variable density distributions. Considering the complete Bouguer effect of a DEM (here the “Bouguer plate” has a finite dimension equal to extension of the source DEM), for the constant density case, it can be obtained immediately from the terrain correction as:

$$\begin{aligned} g_{z}^{cb}(x,y,H)= g_{z}^{\Omega }(x,y,H) - g_{z}^{tc}(x,y,H), \end{aligned}$$

(11)

where $g_{z}^{\Omega }$ represents the $g_z$ effect caused by a rectangular prism with horizontal dimension equal to the integration area $\Omega$, and vertical extension [H, 0] changes according to the position of the computation point. For the more general case when horizontal density variations are allowed, however, it becomes more complicated to start from the terrain correction formulation. In this case, the complete Bouguer effect can be computed directly as:

$$\begin{aligned} g_{z}^{cb}(x,y,H)= & {} G\int _{Y1}^{Y2}\int _{X1}^{X2} \rho (\tilde{x},\tilde{y}) \left[ \int _{h}^{0}\frac{\partial }{\partial z}\left( \frac{1}{R}\right) d\tilde{z} \right] d\tilde{x} d\tilde{y}. \end{aligned}$$

(12)

Solving the integration within the brackets leads to a new kernel function:

$$\begin{aligned} \mathcal {K}_{g_z}^{cb}(L,H,h)=\int _{h}^{0}\frac{\partial }{\partial z}\left( \frac{1}{R}\right) d\tilde{z} =\frac{1}{\sqrt{L^2+(H-h)^2}} - \frac{1}{\sqrt{L^2+H^2}}. \end{aligned}$$

(13)

Applying CP decomposition to $\mathcal {K}_{g_z}^{cb}$ we arrive at:

$$\begin{aligned} \bar{g}_{z}^{cb}(x,y,H) \approx G \sum _{n=1}^{N_{CP}} \lambda _n B_n(H) \Big ( \big [ \rho (\tilde{x},\tilde{y})C_n(h) \big ] * A_n(L) \Big ). \end{aligned}$$

(14)

Here $A_n(L)$, $B_n(H)$ and $C_n(h)$ represent a CP decomposition of $\mathcal {K}_{g_z}^{cb}$ (Eq. 13). Obviously, they change according to different kernel functions. The density function $\rho (\tilde{x},\tilde{y})$ is combined with $C_n(h)$ since both are functions of source coordinates $(\tilde{x},\tilde{y})$. For brevity, we summarize kernel functions and their corresponding CP-FFT expressions for other gravitational components in Appendix 1.

2.4 Magnetic Terrain Effects

Once we have obtained the anomalous GGT:

$$\begin{aligned} \varvec{\Gamma }= \begin{pmatrix} T_{xx} &{} T_{xy} &{} T_{xz} \\ T_{yx} &{} T_{yy} &{} T_{yz} \\ T_{zx} &{} T_{zy} &{} T_{zz} \end{pmatrix}, \end{aligned}$$

(15)

the magnetic terrain effects can be obtained immediately through the Poisson’s relation (Pedersen et al. 2015):

$$\begin{aligned} B_{e}=\frac{\mu _0}{4\pi }\frac{M}{G\rho }\hat{\varvec{e}}^T \varvec{\Gamma } \hat{\varvec{M}}, \end{aligned}$$

(16)

where $\mu _0=4\pi \times 10^{-7}$ H/m is the magnetic permeability of free space, $B_{e}$ is the anomalous magnetic field along the direction $\hat{\varvec{e}}$, $\rho$ is the constant terrain density, $\hat{\varvec{M}}$ and M are the unit direction and magnitude of the assumed homogeneous magnetization. In this case, only 6 GGT components need to be calculated by using the symmetric property of $\varvec{\Gamma }$.

For a general case when the magnetization vector $\varvec{M}$ changes arbitrarily throughout the region: $\varvec{M}=\Big (M_x(\tilde{x},\tilde{y}),M_y(\tilde{x},\tilde{y}),M_z(\tilde{x},\tilde{y})\Big )$, which usually happens when both induced and remnant magnetizations are present (Liu et al. 2018), we have:

$$\begin{aligned} B_{e}= \hat{\varvec{e}} \cdot \varvec{B}, \end{aligned}$$

(17)

with $\varvec{B}=(B_x,B_y,B_z)$ the anomalous magnetic vector that can be computed as:

$$\begin{aligned} B_{x}= & {} \frac{\mu _0}{4\pi G}\left( T_{xx}^{M_x}+T_{xy}^{M_y}+T_{xz}^{M_z}\right) , \end{aligned}$$

(18)

$$\begin{aligned} B_{y}= & {} \frac{\mu _0}{4\pi G}\left( T_{yx}^{M_x}+T_{yy}^{M_y}+T_{yz}^{M_z}\right) , \end{aligned}$$

(19)

$$\begin{aligned} B_{z}= & {} \frac{\mu _0}{4\pi G}\left( T_{zx}^{M_x}+T_{zy}^{M_y}+T_{zz}^{M_z}\right) . \end{aligned}$$

(20)

Here $T_{xx}^{M_x}$, $T_{yx}^{M_x}$ and $T_{zx}^{M_x}$ represent the GGT components $T_{xx}$, $T_{yx}$ and $T_{zx}$ induced by a distribution of density $\rho (\tilde{x},\tilde{y})$ equivalent to the magnetization component $M_x(\tilde{x},\tilde{y})$, respectively. Other quantities can be understood analogously. In this case, a total of 9 GGT components (induced by 3 different variable density sources) need to be evaluated to compute the anomalous magnetic field.

2.5 Accelerating Inner Zone Computation Using a Gaussian Quadrature Mass Line (GQML) Model

The CP-FFT algorithm derived above offers a fast and stable computation of the outer zone effect. However, even for a small separating radius of $R_{FFT}=2$ km, a direct evaluation of the analytical prismatic solution (Nagy et al. 2000) may still be time-consuming for computing high-resolution DEMs (e.g., 90 m resolution or higher). A numerical quadrature solution based on the trapezoidal and Simpson’s rules that is sufficiently accurate with respect to the exact analytical prismatic solution, but which can reduce the computation time by almost 50 per cent is introduced in Goyal et al. (2020). Here we apply a Gaussian quadrature mass line (GQML) model with variable order according to different horizontal distances between the computation point and the integration element. The GQML model is simply to carry out the 3D volume integrals of the gravitational kernels using analytical integration along the vertical dimension, and 2D Gaussian quadrature along the two horizontal dimensions. The idea is similar to the algorithm used in Goyal et al. (2020), we made a modification by applying Gaussian quadrature instead of trapezoidal or Simpson quadratures, and extended to all gravitational components.

Fig. 2

Gaussian quadrature mass line (GQML) approximation of the mass prism model

Figure 2 shows details of the GQML model for each computation point (indicated by a red star) for a typical mid-latitude SRTM v4.1 DEM data with spatial resolution $a=90$ m (along south-north direction), and $b=a\cos (30^{\circ })\approx 80$ m (along west-east direction). Depending on the distance R from the center of a grid cell to the computation point, the closest zone with $R<R_1=a$ is calculated using directly the rigorous prismatic analytical solution (yellow rectangles, normally only 3 prisms needs to be calculated). Gaussian quadrature of orders $N_{GQ}=4^2=16$, $N_{GQ}=2^2=4$ and $N_{GQ}=1^2=1$ are used to approximate the prismatic analytical solution in the near zone $R \in [R_1,R_2)=[a,3a)$ (dark blue), intermediate zone $R \in [R_2,R_3)=[3a,10a)$ (blue), and distant zone $R \in [R_3,R_{FFT})=[10a,R_{FFT})$ (light blue), respectively. The region with $R \ge R_{FFT}=2$ km is computed by the CP-FFT algorithm (red zone).

Fig. 3

Change in relative errors $\vert \epsilon \vert$ with respect to distance/length ratio L/a, height/length ratio of the prism c/a, and different orders $N_{GQ}$ of the Gaussian quadrature mass line (GQML) model in approximating the analytical prismatic solution of $g_z$

Figure 3 shows changes in relative errors $\vert \epsilon \vert$ of the Gaussian quadrature mass line (GQML) model in approximating the analytical prismatic solution of $g_z$ with respect to several parameters, including (1) the distance/length ratio L/a, (2) height/length ratio of the prism c/a, and (3) order of the GQML $N_{GQ}$. It can be observed that by choosing the parameters described above, generally a relative error of $\vert \epsilon \vert \le 10^{-3}$ can be guaranteed for prismatic bodies with various geometries (a height/length ratio of $c/a=100$ represents a prism with length 90 m and height 9000 m, while a height/length ratio of $c/a=0.1$ represents a prism with length 90 m and height 9 m, the width of the prism is fixed as $b\approx 80$ m as has been mentioned above).

Numerical behavior of the GQML approximation for other gravitational components, including the GP, the other two GV components, and the GGT components are similar. Smaller relative errors are obtained for the GP component (generally below $10^{-4}$), and larger relative errors $\vert \epsilon \vert >10^{-2}$ occur for GGT components only when the magnitude of the referenced value is very small ($<10^{-3}$ E$\ddot{o}$tv$\ddot{o}$s), thus is negligible in a practical modeling procedure. Based on these numerical results, we have chosen the same set of GQML model parameters for all gravitational components.

3 Numerical Examples and Results

We test the numerical performance of our CP-FFT method by using space-domain mass line (Li and Sideris 1994) or mass prism solutions (Nagy et al. 2000) as the precise references. The $l_2$-norm relative error $E_2$ is applied as an overall estimation of the numerical accuracy (Wu 2021). Computational time costs $t_{ref}$ and $t_{cp}$ for both methods, together with the acceleration ratio $\tau =t_{ref}/t_{cp}$, are provided for verification of numerical efficiency. It should be noted that the computer code for space-domain solutions have also been properly optimized to achieve maximum speed. The experiments are carried out on a platform with Intel Core $i7-9850H$ 2.6 GHz and 64 GB RAM, and implemented in MATLAB R2020b software.

Numerical experiments are arranged as follows: (1) In Sect. 3.1, we use a simple mass line model (SML) to test the accuracy and efficiency of our CP-FFT method for outer-zone computation, as for the inner-zone computation, both methods apply the space-domain mass line solution. Based on the numerical results obtained in Sect. 3.1, we carry out further numerical tests in Sect. 3.2 and provide empirical choice for parameters of our algorithm for different topographic models. (2) In Sect. 3.3, we take a step further to include a Gaussian quadrature mass line (GQML) model for inner-zone computation, and compare our method to the more rigorous rectangular prism solution. Therefore, numerical approximations are made for both inner/outer-zone calculations. Computation surfaces, both on, above and below the topography are tested. (3) In Sects. 3.4 an 3.5, numerical examples are designed to demonstrate the validity of our algorithm for computing terrain-induced terrestrial and airborne gravitational effects, including all GP, GV and GGT components, and for magnetic terrain effects, with variable density/magnetization taken into account.

3.1 Simple Mass Line (SML) Model Tests

Fig. 4

DEMs (first column, unit in km) and the corresponding forward results of $g_z^{cb}$ (in mGal) over 4 selected mountainous areas around the globe using space-domain rigorous solution of mass lines (second column) and the CP-FFT algorithm (third column). Test areas include Himalayas (first row), Andes (second row), European Alps (third row) and Australian Alps (fourth row). Blue rectangles indicate calculation areas, red lines indicate two profiles (A and B) crossing the highest peaks of each test area

First we test our new algorithm using a simple mass line (SML) model, where each prismatic grid cell is approximated using a single mass line at its center. Four patches of $2^{\circ } \times 2^{\circ }$ SRTM v4.1 data with $3'' \times 3''$ resolution (Jarvis et al. 2008), including Himalayas, Andes, European Alps and Australian Alps, are used as the input topographic data source. Planar approximations are applied by letting $\Delta x=3'' \chi$, $\Delta y=3'' \chi \cos (\varphi _m)$, where $\varphi _m$ is the mean latitude of the patch and $\chi$ is the arcseconds-to-kilometres conversion factor for a sphere of radius $R_e=6378.137$ km. A constant density $\rho =2670$ kg/m$^3$ is assumed.

We apply CP decomposition to the terrain correction kernel $\mathcal {K}_{g_z}^{tc}$ (Eq. 5), the complete Bouguer effects are calculated by adding to the terrain correction effects the contribution of a “regional prism” (see Eq. 11). Parameters of the CP-FFT algorithm are chosen as $N_L=N_H=N_h=100$, $R_{FFT}=2$ km, and $N_{CP}=50$. Gravity values are calculated right above the topography. As shown in Fig. 4, almost identical forward results are obtained, with maximum absolute errors (MAEs) below 1 mGal, root mean square (RMS) errors below 0.15 mGal, and $E_2$ errors below 0.1% for all selected mountainous regions. More statistical details of the results are summarized in Table 1. The space-domain solution takes more than 20 days to complete the whole calculation (4 patches, each with source grid $2400 \times 2400$, computation grid $2160 \times 2160$). The CP-FFT algorithm, on the other hand, costs only about 9 minutes (acceleration $\tau >3000$), proving its huge advantage in computational efficiency.

Table 1 Descriptive statistics of the topography height values, the forward results of $g_z^{cb}$ calculated using both the mass line analytical solution (reference) and the CP-FFT algorithm, with the corresponding differences between the two algorithms over 4 selected test areas shown in Fig. 4. Elevation values in km (positive upward), $g_z^{cb}$ values in mGal

3.2 Empirical Choice for the Parameters of the CP-FFT Algorithm

Fig. 5

Error level changes with respect to increasing rank of CP decomposition $N_{CP}$ and different separating radius $R_\mathrm{{FFT}}$ (in km) for the modeling of $g_z$ field induced by the chosen 4 test areas: a Himalayas, b Andes, c European Alps and d Australian Alps. MAE stands for maximum absolute error, RMS stands for root mean square error

Although we have chosen parameters of the CP-FFT algorithm as $R_\mathrm{{FFT}}=2$ km and $N_{CP}=50$ in all numerical tests implemented above, it should be noted that for a DEM with less change in height values, a lower rank of CP decomposition ($N_{CP}$) and a smaller separating radius ($R_\mathrm{{FFT}}$) may be adequate to provide forward results with sufficiently high accuracy in less computation time.

Figure 5 shows changes in maximum absolute errors (MAE) and root mean square (RMS) errors (in mGal) with respect to different separating radius and increasing CP decomposition ranks for the modeling of the gravitational component $g_z$ caused by the chosen 4 test areas around the globe with different topographic elevation differences: (a) Himalayas (about 9 km), (b) Andes (about 6 km), (c) European Alps (about 4.5 km) and (d) Australian Alps (about 2 km). The numerical results can be summarized as follows:

• i) Increasing the separating radius ($R_\mathrm{{FFT}}$) always improves accuracy, albeit at the computational expense of more time-consuming space-domain inner zone evaluation.

• ii) Ideally, convergence should be guaranteed no matter what $R_\mathrm{{FFT}}$ is chosen. However, it can be observed in Fig. 5 that when $R_\mathrm{{FFT}}$ is chosen small comparing to the overall height change in the DEM, e.g., $R_\mathrm{{FFT}}=1$ km for the Himalayas region, convergence of the algorithm slow down significantly. This may be caused by the intrinsic difficulty in approximating the gravitational kernel for near-field effect using CP decomposition.

• iii) Increasing the rank of CP decomposition ($N_{CP}$) generally also improves the accuracy, however, the accuracy no longer improves after a certain threshold is reached. Besides, due to the randomness of the CP decomposition, some irregular jumps of the MAE and RMS errors can be observed, but the overall trend is not affected.

• iv) The results in Fig. 5 can serve as a reference for parameter selection criterion of the CP-FFT algorithm for computing terrain-induced gravitational fields in other mountainous regions. We recommend a selection of $R_{FFT}=\frac{\max (h)-\min (h)}{4}$, and $N_{CP}=50$, for which MAE below 1 mGal, and RMS below 0.1 mGal can be achieved.

Fig. 6

Error level changes with respect to increasing rank of CP decomposition $N_{CP}$ using a pure FFT algorithm in the Himalayas test area. Here $R_{FFT}=0.05$ km is chosen to completely avoid the analytical calculation of the inner-zone effect. MAE stands for maximum absolute error, RMS stands for root mean square error

To explore more convergence characteristics of the CP-FFT method, we carried out further numerical tests using an extreme value of the parameter $R_\mathrm{{FFT}}=0.05$ km in the Himalayas test area. In this case, even the nearest mass line element (at a distance about 0.08 km) is excluded from the inner-zone calculation for each computation point, which means we now have a pure FFT algorithm over the entire region. We also choose three different values of $N_{LHh}=100$, 200, 300, where $N_{LHh}=N_{L}=N_{H}=N_{h}$ is the dimension of the CP decomposition, to test the effect of this parameter on the final accuracy.

Figure 6 shows error level changes as the rank of CP decomposition $N_\mathrm{{CP}}$ increases from 100 to 1000, and dimension of the CP decomposition $N_{LHh}$ increases from 100 to 300. We summarize the numerical results as follows:

• (i) Ideally, for the same computation area, larger values of $N_L$, $N_H$, $N_h$ would provide more accurate results. However, numerical tests show that the approximation accuracy reaches a certain limit when the values of $N_L$, $N_H$, $N_h$ are large enough. After that, further increasing the value cannot effectively reduce the error, but brings more computation. The inherent randomness of the CP decomposition function cp_als brings some uncertainty, larger parameters do not necessarily give better results, it may even reduce the accuracy in some cases.

• (ii) The pure FFT method converges rather slowly, even by using a large value of $N_\mathrm{{CP}}=1000$, we still have MAEs and RMS errors above 1 mGal in all cases. This suggests that by applying the current CP decomposition algorithm, we still can not obtain an accurate global approximation of the gravitational kernel. Therefore, inner-zone computation using space-domain solution is still necessary to guarantee a sub-mGal level accuracy in the most mountainous areas of the Earth.

We also made a rough estimate of the computation time of our CP-FFT algorithm as a function of grid sizes, CP decomposition rank, and the separating radius based on the results obtained above. As shown in Fig. 7, computation time increases linearly with $N_\mathrm{{CP}}$, and quadratically with $R_\mathrm{{FFT}}$, the relation can be estimated as:

$$\begin{aligned} t=c_0+c_1 \hat{N}\log (\hat{N}) N_{CP} + c_2 \frac{N_x N_y}{\Delta x \Delta y} R_{FFT}^2, \end{aligned}$$

(21)

where $\hat{N}=(N_x+\tilde{N}_x)(N_y+\tilde{N}_y)$ is the size of the 2D FFT implemented in calculating the outer-zone effect, $\tilde{N}_x \times \tilde{N}_y$ is the size of the topographic source grid, $N_x \times N_y$ is the size of the computation grid, $\Delta x \times \Delta y$ is the dimension of a grid cell, and $\frac{N_x N_y}{\Delta x \Delta y} R_\mathrm{{FFT}}^2$ is proportional to the number of mass lines required in evaluating the inner-zone effect for an SML model.

The estimated values for $c_0$, $c_1$ and $c_2$ given by a least square fitting are: $c_1\approx 5.2 \times 10^{-9}$, $c_2 \approx 1.6 \times 10^{-8}$, and $c_0\approx 2.5$ on our platform. We mention that for the GQML model implemented in the following, the computation amount does not change for the outer-zone evaluation, however, the number of mass lines required for the inner-zone computation would be approximately 1 to 3 times larger than that of the SML model. Therefore, a rough estimation of $c_2^{GQML} \approx 2 c_2^{SML}$ can be applied for time estimation of a CP-FFT algorithm combined with a GQML approximation of the mass prism model.

Fig. 7

Time costs of the CP-FFT algorithm estimated as a function of the rank of CP decomposition $N_\mathrm{{CP}}$ and the separating radius $R_\mathrm{{FFT}}$, with estimation errors and associated statistics (minimum, maximum and root-mean-square) shown in the histogram

3.3 Gaussian Quadrature Mass Line Model Tests

Next we evaluate the analytical prismatic solution (Nagy et al. 2000) as the precise reference, and combine our CP-FFT algorithm with a Gaussian quadrature mass line (GQML) model to speed up the inner zone computation with controlled accuracy. Each prismatic grid cell is now approximated using multiple mass lines formulating a 2D Gaussian quadrature. Depending on the attenuation of the gravitational fields with distance, the order of the Gaussian quadrature is chosen as $N_{GQ}=16$, 4, and 1 in the near, intermediate and distant zone, respectively, to guarantee a relative error of $\vert \epsilon \vert \le 10^{-3}$ (see Fig. 2).

Fig. 8

Forward results of $g_z^{cb}$ on two profiles crossing the highest peak of the Himalayas test area with multiple computation heights D. a Elevation changes along the two profiles (red lines A and B in Fig. 4, first row). Forward results using both the rigorous prism-summation (PS) method (red and blue solid lines) and the CP-FFT method (yellow and cyan dash-dot lines) are compared on 8 different observation heights (only 4 are shown here) parallel to the topography with a distance D, with b $D=0$ m representing the topography itself, c $D=2000$ m simulating typical flight heights for airborne surveys, and d $D=-500$ m, e $D=-5000$ m indicating underground computation profiles. Statistical details for all 8 computation heights are summarized in Table 2

Table 2 Descriptive statistics of the forward results of $g_z^{cb}$ in Fig. 8. Comparisons are made on 8 different observation heights parallel to the topography, with $D=0$ m representing the topography itself, $D=500,1000,2000$ m above the topography, and $D=-500,-1000,-2000,-5000$ m below the topography. Gravity values in mGal

As shown in Fig. 8, $g_z^{cb}$ effects of the Himalayas test area are calculated and compared on 8 different observation heights parallel to the topography with distance $D=0,500,1000,2000,-500,-1000,-2000,-5000$ m (positive/negative D indicate computation surface above/below the topography). The CP-FFT method is implemented using directly the CP decomposition of the $\mathcal {K}_{g_z}^{cb}$ kernel (Eq. 13). The prism-summation (PS) solution is computed only along two profiles (A and B in Fig. 4) for reference due to the enormous computational costs. Almost identical forward results are obtained, with MAEs below 2 mGal, RMS errors below 0.5 mGal, and $E_2$ errors below 0.2% for all chosen observation heights. More statistical details can be found in Table 2. The space-domain solution takes more than 16 hours computing results simply on two profiles, while the CP-FFT algorithm takes only about 36 minutes computing all 8 observation surfaces (acceleration $\tau >20000$), showing its capability for high-efficiency computation of terrain-induced gravitational fields on arbitrary undulating surfaces.

Fig. 9

Forward results of $T_{zz}^{cb}$ on two profiles crossing the highest peak of the European Alps test area with multiple computation heights D. a Elevation changes along the two profiles (red lines A and B in Fig. 4, third row). Forward results using both the rigorous prism-summation (PS) method (red and blue solid lines) and the CP-FFT method (yellow and cyan dash-dot lines) are compared on 8 different observation heights (only 4 are shown here) parallel to the topography with a distance D, with b $D=1$ m above the topography, c $D=100$ m, d $D=1000$ m and e $D=5000$ m simulating typical flight heights for airborne surveys. Statistical details for all 8 computation heights are summarized in Table 3

Table 3 Descriptive statistics of the forward results of $T_{zz}^{cb}$ in Fig. 9. Comparisons are made on 8 different observation heights parallel to the topography, with $D=1,5,10,50,100,500,1000,5000$ m all above the topography. Units in Eötvös

Similar comparisons are made for the $T_{zz}^{cb}$ component on two profiles crossing the highest peak of the European Alps test area at various heights $D=1,5,10,50,100,500,1000,5000$ m above the topography. As shown in Fig. 9, again, almost identical forward results are obtained, with MAEs below 2 E$\ddot{o}$tv$\ddot{o}$s, RMS errors below 1 E$\ddot{o}$tv$\ddot{o}$s, and $E_2$ errors below 0.3% for all chosen observation heights. More statistical details can be found in Table 3. The space-domain solution takes about 4.5 hours computing results simply on two profiles, while the CP-FFT algorithm takes only about 1 hour computing all 8 observation surfaces. Here an acceleration ratio of $\tau >5000$ is achieved. Comparing with the time costs for computing $g_z^{cb}$, space-domain solution accelerates about 3 times due to simpler expressions (Nagy et al. 2000), while the CP-FFT solution slows down slightly due to increased complexity of the analytical mass line expressions (see Appendix 1, $J_1$ and $J_2$ expressions).

3.4 GP, GV and GGT Modeling with Laterally Variable Density

Fig. 10

a $3'' \times 3''$ resolution SRTM v4.1 DEM (Jarvis et al. 2008) of the Colorado test area and selected terrestrial (blue triangles) and airborne (red diamonds) gravity observation locations. b Laterally variable density distribution interpolated from the $30''$ resolution UNB_TopoDens model (Sheng et al. 2019). c Interpolated terrain clearance D. d The calculation surface $H_\mathrm{{cal}}=h_{DEM}+D$. e CP-FFT calculated $g_z$ component. f CP-FFT calculated $T_{zz}$ component. Height values in meters, density in kg/m$^3$, $g_z$ values in mGal, and $T_{zz}$ in E$\ddot{o}$tv$\ddot{o}$s

We now test our CP-FFT algorithm for a complete modeling of GP, GV, GGT components caused by a large DEM with laterally variable density. As shown in Fig. 10, the area bordered by latitude $35^{\circ }$N to $40^{\circ }$N and longitude $110^{\circ }$W to $102^{\circ }$W, which was applied in the Colorado 1-cm geoid computation experiment (Wang et al. 2021) for a comparison study of numerous geoid computation methods used by different groups around the world, is adopted here for numerical validation.

The input topographic dataset is the SRTM v4.1 DEM with a spatial resolution of $3''$ and a total grid size of $9601 \times 6001$. The input $3''$ resolution laterally variable density grid is obtained from linear interpolating the $30''$ resolution UNB_TopoDens model (Sheng et al. 2019), which is transformed from the Global Lithology Model (GLiM) (Hartmann and Moosdorf 2012) by assigning probable surface density values to the lithologies based on geological data. The density value varies between a minimum of 1000 kg/m$^3$, indicating lakes within the area, and a maximum of 2854 kg/m$^3$, slightly above the normally applied mean topographic density value 2670 kg/m$^3$ (see Fig. 10b). It should be noted that since vertical variation of density is not considered, the laterally variable density model used here is more to validate our algorithm than as a better approximation to the real density distribution.

As shown in Fig. 10a, a subset of 7991 gravity observations, with 3906 terrestrial ones and 4085 airborne ones (randomly picked with generally equal distance), are selected from the gravity datasets used in the Colorado geoid computation experiment (Wang et al. 2021). For the terrestrial gravity dataset, only observations above the input DEM (with terrain clearance $D=H_{cal}-h_{DEM} \ge 0$) are kept. Nevertheless, we still get D values vary from 0 m to a maximum of 535 m, which is clearly unrealistic for land gravity observations. These may be caused by height errors from either the DEM or the gravity dataset, we leave these unchanged to cover forward modeling situations when airborne surveys are carried out on a typical height of several hundred meters above topography in flat areas (Pedersen et al. 2015). For airborne observations, terrain clearance D changes vastly from about 1300 m to 6400 m, which is more than adequate to cover most practical airborne modeling situations.

The calculation surface $H_{cal}$ (see Fig. 10d) is constructed as follows: first the terrain clearance values D of the picked 7991 gravity observations are interpolated to a regular grid identical to the DEM dataset using a nearest-neighbor method (see Fig. 10c), then the calculation surface is obtained from $H_{cal}=h_{DEM}+D$, where $h_{DEM}$ denotes the DEM height of the grid point, and D is the interpolated terrain clearance value at the grid point.

Fig. 11

Difference maps for GP, GV and GGT components between CP-FFT forward results and prism-summation computed reference values at the selected 7991 gravity observations in Fig. 10a. GP values in m$^2$/s$^2$, GV values in mGal, GGT values in E$\ddot{o}$tv$\ddot{o}$s

The CP-FFT method is applied for the computation of all GP, GV and GGT components on the undulating calculation surface. Due to the increased horizontal extents of both the source and the computation grids, and the large vertical extent of the observations ($H_{cal} \in [1028,9195]$ m), parameters of the CP-FFT algorithm are chosen as $N_L=N_H=N_h=200$, $R_{FFT}=2$ km, and $N_{CP}=60$ here. The obtained $g_z$ and $T_{zz}$ components are shown in Fig. 10e and f, respectively. It can be observed that $g_z$ field in the airborne region (red zone in Fig. 10c) is somehow a low-pass filtered version of the terrestrial field (blue zone in Fig. 10c), and both have a strong correlation with the DEM. The $T_{zz}$ component, which is a high-pass filtered version of the $g_z$ filed, clearly contains more short-wavelength information, especially for the terrestrial observations. (Note here we choose limits $[-100,100]$ E$\ddot{o}$tv$\ddot{o}$s for the color bar to show more details of the $T_{zz}$ field, the actual limits are $[-1100,1462]$ E$\ddot{o}$tv$\ddot{o}$s, see Table 4).

For precise reference, the prism-summation (PS) solution is computed at the selected 7991 gravity observations (see Fig. 10a). Figure 11 shows difference maps of all GP, GV and GGT components between the two applied algorithms at the selected observations. More statistical details are summarized in Table 4. Obviously, the two algorithms agree perfectly, with $E_2$ errors below 0.01%, 0.1% and 1.3% for the GP, GV and GGT components, respectively. Specifically, we have MAE as 0.1 mGal, RMS error as 0.05 mGal, $E_2$ error as 0.02% for the $g_{z}$ component, and MAE below 1 E$\ddot{o}$tv$\ddot{o}$s, RMS error below 0.1 E$\ddot{o}$tv$\ddot{o}$s, $E_2$ error below 0.1% for the $T_{zz}$ component. Except for the $T_{xx}$ and $T_{yy}$ components, which exhibit slightly larger errors (MAE about 6 E$\ddot{o}$tv$\ddot{o}$s), MAEs for other GGT components are generally below 1 E$\ddot{o}$tv$\ddot{o}$s, which is sufficiently accurate for most practical applications. The space-domain solution takes more than 5 days computing values simply at the subset of 7991 observations, while the CP-FFT algorithm takes about 16 hours computing all 10 gravitational components on the size $9601 \times 6001$ computation grid (acceleration $\tau >60000$), proving its capability for fast computation of gravitational signal induced by large DEM datasets on personal computers.

Table 4 Statistics of the forward results of GP, GV and GGT components caused by the Colorado DEM model with laterally variable density (see Fig. 10) using CP-FFT and prism-summation algorithms. GP in m$^2$/s$^2$, GV in mGal, and GGT in E$\ddot{o}$tv$\ddot{o}$s

3.5 Magnetic Field Modeling

Fig. 12

Comparison of space-domain and CP-FFT forward results of sea surface and near-bottom magnetic fields induced by a bathymetric model with variable magnetization around $13^{\circ }$N on the Mid-Atlantic Ridge. a Bathymetry of the area. b Inverted seafloor magnetization digitized from Searle et al (2019, Fig. 5) c–e Sea surface magnetic anomaly $B_e^{SS}$ calculated by using space-domain and CP-FFT algorithms and the corresponding difference. (f–h) Near-bottom magnetic anomaly $B_e^{NB}$ calculated by using space-domain and CP-FFT algorithms and the corresponding difference. Bathymetry values in meters, magnetization in A/m, magnetic fields in nT

The final example is dedicated to the modeling of magnetic fields induced by a bathymetric model around $13^{\circ }$N on the Mid-Atlantic Ridge, where sea surface gravity, magnetic data, and near-seafloor magnetic fields have been measured and analyzed by several authors for the study of oceanic core complexes (OCC) (Mallows et al. 2012; Searle et al. 2019). As shown in Fig. 12, a patch of $0.5^{\circ } \times 0.5^{\circ }$ multibeam bathymetry data with $3'' \times 3''$ resolution is downloaded from NOAA’s National Centers for Environmental Information (NCEI). To test our new algorithm for variable magnetization, we apply the inverted seafloor magnetization in Searle et al. (2019) in our forward modeling.

The computations are carried out both at the sea surface and at an undulating surface with 100 m constant height above the seafloor. The magnetic fields are induced from a 0.5 km thick source layer with either normally (positive magnetization) or reversely (negative magnetization) magnetized blocks. The magnetization is in the direction of a geocentric axial dipole with declination $0^{\circ }$, inclination $25.6^{\circ }$ (Searle et al. 2019), and the background magnetic direction is calculated from the IGRF-13 model as declination $-17^{\circ }$, inclination $21^{\circ }$ (Alken et al. 2021).

Using the prismatic solution as the precise reference, our CP-FFT algorithm ($N_L=N_H=N_h=100$, $R_{FFT}=2$ km, $N_{CP}=50$) obtains MAEs below 1 nT, RMS errors below 0.2 nT, and $E_2$ errors below 0.3% for sea surface magnetic field modeling, and MAEs below 7 nT, RMS errors below 2 nT, and $E_2$ errors below 0.7% for all near-bottom magnetic vector components. More statistical details can be found in Table 5. The space-domain solution takes more than 2 days to complete the whole calculation (source grid size $601 \times 601$, computation grid size $591 \times 591$), while the CP-FFT algorithm costs only about 17 minutes (acceleration $\tau \approx 190$), proving its remarkable efficiency in computing magnetic components on both constant and undulating surfaces caused by densely-sampled, rough bathymetric models with variable magnetization.

Table 5 Descriptive statistics of the forward results of magnetic effects of the bathymetric model in Fig. 12. SS stands for Sea Surface magnetic fields, and NB stands for Near Bottom magnetic fields. Units in nT

4 Conclusions

In this study, we have developed a new CP-FFT algorithm for fast and accurate computation of topographic gravitational and magnetic fields. We have made several improvements to the classical FFT-based terrain correction algorithm, including (a) CP decomposition instead of binomial expansion is applied to guarantee the convergence of the outer zone computation for rough terrain or bathymetry models, (b) the new method is extended to include GP, GV, GGT and magnetic field forward modeling on arbitrary undulating surfaces caused by topographic sources with variable density/magnetization, and (c) a GQML model is introduced to accelerate the computation of the inner zone effect. Numerical tests prove that our new algorithm has great advantage in computational speed over space-domain solutions while maintaining a sufficiently high accuracy well below existing instrumentation error levels.

Except for the sizes of the source and computation grids, computational efficiency of the new algorithm mainly depends on $R_{FFT}$, i.e., the radius separating the inner and outer computation zones. A larger separating radius would require more time-consuming space-domain evaluation of inner-zone effects, while in the mean time accelerate the convergence of the outer-zone calculation. An empirical value of $R_{FFT}=\frac{\max (h)-\min (h)}{4}$, which equals to one fourth of the overall undulation of the input DEM, is recommended to better balance computational efficiency and accuracy. Besides, a value of $N_{CP}=50$ for CP decomposition of the gravitational integration kernels is also recommended for the FFT-evaluated outer-zone effect to achieve sufficient accuracy with minimum computation amount. For the dimension of the CP decomposition, we recommend using $N_L=N_H=N_h=100$ for computation areas at a scale of around $200 \times 200$ km, and $N_L=N_H=N_h=200$ for computation areas at a scale of around $500 \times 500$ km. For calculation areas above 500 km, the influence of Earth curvature may become more significant, and the CP-FFT method may not be applicable.

The proposed method is developed in Cartesian coordinates, therefore, it should be used with caution when dealing with regional gravitational or magnetic modeling problems where planar approximation of the actual curved Earth can lead to significant errors. Extension of the method to include the curvature of the Earth through a resampling of the DEM may be possible. However, since most DEM products are provided on geographical grids, additional Cartesian-Spherical coordinate transformations and interpolations of both the DEM and the calculated fields are required to obtain forward results also on geographical grids.

In our numerical tests, the inner zone effect is evaluated using prismatic solutions, with the topography represented by a step function. Using a more smooth polyhedral or bilinear representation of the topography for evaluation would certainly improve the accuracy of modeling. The computational cost will be slightly increased by choosing different height values for each mass line in our GQML model using triangular or bilinear interpolation within each grid cell. These may be treated in an updated version of our algorithm and computer code.

The new algorithm may be a ready substitute for existing methods. All source codes, including space-domain solutions, the CP-FFT algorithm, and several numerical examples, are released in MATLAB language. To our knowledge, there is no publicly available code that effectively and efficiently implements similar forward computing capabilities, which covers terrain-induced GP, GV, GGT and magnetic fields on arbitrary undulating surfaces, and takes into account variable density/magnetization distributions.

Appendix 1 CP-FFT Expressions for GP, GV, GGT with Horizontal Variable Density

Kernel functions for the gravitational potential (GP) V:

$$\begin{aligned} \mathcal {K}_{V}^{cb} = \int _{h}^{0} \frac{1}{R} d\tilde{z}=I_1. \end{aligned}$$

(22)

For the gravitational vector (GV) components $g_x$, $g_y$, $g_z$:

$$\begin{aligned} \mathcal {K}_{g_x}^{cb}= & {} \frac{\partial }{\partial x} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) =(x-\tilde{x}) I_2, \end{aligned}$$

(23)

$$\begin{aligned} \mathcal {K}_{g_y}^{cb}= & {} \frac{\partial }{\partial y} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) =(y-\tilde{y}) I_2, \end{aligned}$$

(24)

$$\begin{aligned} \mathcal {K}_{g_z}^{cb}= & {} \frac{\partial }{\partial z} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) =J_1. \end{aligned}$$

(25)

For the gravitational gradient tensor (GGT) components $T_{xx}$, $T_{xy}$, $T_{xz}$, $T_{yy}$, $T_{yz}$, $T_{zz}$:

$$\begin{aligned} \mathcal {K}_{T_{xx}}^{cb}= & {} \frac{\partial ^2}{\partial x^2} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) = 3(x-\tilde{x})^2 I_3+I_2, \end{aligned}$$

(26)

$$\begin{aligned} \mathcal {K}_{T_{xy}}^{cb}= & {} \frac{\partial ^2}{\partial x \partial y} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) = 3(x-\tilde{x})(y-\tilde{y}) I_3, \end{aligned}$$

(27)

$$\begin{aligned} \mathcal {K}_{T_{xz}}^{cb}= & {} \frac{\partial ^2}{\partial x \partial z} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) = (x-\tilde{x}) J_3, \end{aligned}$$

(28)

$$\begin{aligned} \mathcal {K}_{T_{yy}}^{cb}= & {} \frac{\partial ^2}{\partial y^2} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) = 3(y-\tilde{y})^2 I_3+I_2, \end{aligned}$$

(29)

$$\begin{aligned} \mathcal {K}_{T_{yz}}^{cb}= & {} \frac{\partial ^2}{\partial y \partial z} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) = (y-\tilde{y}) J_3. \end{aligned}$$

(30)

$$\begin{aligned} \mathcal {K}_{T_{zz}}^{cb}= & {} \frac{\partial ^2}{\partial z^2} \left( \int _{h}^{0} \frac{1}{R} d\tilde{z} \right) = J_2. \end{aligned}$$

(31)

Here

$$\begin{aligned} I_1= & {} \ln \frac{\sqrt{L^2+(H-h)^2}+(H-h)}{\sqrt{L^2+H^2}+H}, \end{aligned}$$

(32)

$$\begin{aligned} I_2= & {} -\frac{1}{L^2} \Big ( \frac{H-h}{\sqrt{L^2+(H-h)^2}} - \frac{H}{\sqrt{L^2+H^2}} \Big ), \end{aligned}$$

(33)

$$\begin{aligned} I_3= & {} -\frac{I_2}{L^2}-\frac{1}{3 L^4} \left[ \left( \frac{H-h}{\sqrt{L^2+(H-h)^2}}\right) ^3 - \left( \frac{H}{\sqrt{L^2+H^2}}\right) ^3 \right] , \end{aligned}$$

(34)

$$\begin{aligned} J_1= & {} \frac{1}{\sqrt{L^2+(H-h)^2}} - \frac{1}{\sqrt{L^2+H^2}}, \end{aligned}$$

(35)

$$\begin{aligned} J_2= & {} \frac{H}{[L^2+H^2]^{\frac{3}{2}}} - \frac{H-h}{[L^2+(H-h)^2]^{\frac{3}{2}}}, \end{aligned}$$

(36)

$$\begin{aligned} J_3= & {} \frac{1}{[L^2+H^2]^{\frac{3}{2}}} - \frac{1}{[L^2+(H-h)^2]^{\frac{3}{2}}}. \end{aligned}$$

(37)

The CP decompositions are applied to the functions $I_i$ or $J_i$, $i=1,2,3$, all of which are functions of (L, H, h). Extra factors $(x-\tilde{x})^i$ or $(y-\tilde{y})^i$, $i=1,2$ can be combined with $A_n(L)$ since both are functions of $(x-\tilde{x},y-\tilde{y})$.

CP-FFT expression for the $g_x$ component is:

$$\begin{aligned} \bar{g}_{x}^{cb}(x,y,H) \approx G \sum _{n=1}^{N_{CP}} \lambda _n B_n(H) \Big ( \big [ \rho (\tilde{x},\tilde{y})C_n(h) \big ] * \big [ (x-\tilde{x}) A_n(L) \big ] \Big ), \end{aligned}$$

(38)

with $A_n(L)$, $B_n(H)$ and $C_n(h)$ representing a CP decomposition of $I_2$.

CP-FFT expression for the $T_{xx}$ component is:

$$\begin{aligned} \bar{T}_{xx}^{cb}(x,y,H)\approx & {} G \sum _{n=1}^{N_{CP}} \lambda _n^{(1)} B_n^{(1)}(H) \Big ( \big [ \rho (\tilde{x},\tilde{y})C_n^{(1)}(h) \big ] * \big [ 3(x-\tilde{x})^2 A_n^{(1)}(L) \big ] \Big ) \nonumber \\+ & {} G \sum _{n=1}^{N_{CP}} \lambda _n^{(2)} B_n^{(2)}(H) \Big ( \big [ \rho (\tilde{x},\tilde{y})C_n^{(2)}(h) \big ] * A_n^{(2)}(L) \Big ), \end{aligned}$$

(39)

with $A_n^{(1)}(L)$, $B_n^{(1)}(H)$ and $C_n^{(1)}(h)$ representing a CP decomposition of $I_3$, and $A_n^{(2)}(L)$, $B_n^{(2)}(H)$ and $C_n^{(2)}(h)$ representing a CP decomposition of $I_2$.

The computation of the GGT components $T_{xx}$ and $T_{yy}$ requires the summation of two CP-FFTs, while all other components can be solved using one single CP decomposition.